Опубликовано в журнале "Менеджмент в России и за рубежом" №4 год - 2009
Михненко П.А.,
к. т. н., доцент,
зав. кафедрой общего
менеджмента Московской
финансово-промышленной
академии
Системный подход к анализу хозяйственных организаций обогатил современный менеджмент понятием «жизненный цикл организации (ЖЦО) – последовательность предсказуемых изменений состояния организации (стадий, этапов) с течением времени. Каждый этап жизненного цикла – набор разнообразных характеристик деятельности организации.
Проблеме изучения жизненного цикла организаций посвящено множество работ. Единой методологии изучения этого процесса нет. Ранее чаще встречались теоретические изыскания. Сейчас авторы ставят ударение на эмпирических подходах и анализе прикладного значения этой концепции [1–6].
Прикладное значение моделей ЖЦО, по-видимому, заключается в том, что ситуационный подход к управлению (иначе говоря, ситуационное мышление менеджера) требует от руководителей чёткого понимания, на каком этапе жизненного цикла находится организация и какие методы управления оптимальны в этой стадии.
Наиболее важным в теории жизненных циклов организации нам представляется следующий вывод: «переходы от одного этапа к другому являются предсказуемыми, а не случайными» [7, с. 52]. Строго говоря, употребление термина «не случайными» не вполне оправданно, поскольку стохастический аспект присущ практически любым сложным процессам, к которым, безусловно, относятся и процессы функционирования социально-экономических систем. Тем не менее стохастическая трактовка смены этапов ЖЦО не отрицает её предсказуемости, она лишь требует привлечения для анализа методов теории вероятностей и математической статистики.
В настоящее время с применением стохастических моделей различных классов изучаются такие аспекты функционирования организаций, как неопределённость внешней среды, погрешности производственных, контрольных и иных операций во внутренней среде. Привлечение таких моделей требуется также для исследования устойчивости, наблюдаемости и управляемости организационных систем.
Задачи исследования развития организаций требуют использования методов теории динамических систем. Наибольшую сложность в ходе стохастического моделирования динамических организационных систем представляет описание разрывных случайных процессов, которые в общем случае не поддаются формализации в рамках традиционных моделей. При этом практика управления современными рыночными структурами, функционирующими в условиях неопредёленного и высокоподвижного внешнего окружения, требует отражения в организационных моделях аспектов случайности и непредсказуемости смены явлений и структур [4; 7; 8]. Переходы организационных систем от одного этапа жизненного цикла к другому тоже относятся к процессам такого типа.
К явлениям и процессам, порождающим стохастичность и неопределённость организационных систем, можно, например, отнести:
- нечёткость целей на начальном этапе развития организации;
- неформальные аспекты коммуникаций и принятия решений, характерные для этапа коллективности;
- поиск направлений развития в условиях высокого уровня конкурентного давления;
- слабую предсказуемость изменений внешней среды, обусловленных политическими и экономическими факторами на международном уровне;
- недостаточную определённость причин снижения основных показателей на этапе спада активности.
С теоретической точки зрения (и этот тезис, как известно, лежит в основе теории вероятностей) случайные факторы ничем не отличаются от «основных» факторов.
Однако попытки выявить огромное число закономерностей неизбежно ведут к возрастанию сложности и громоздкости аналитических процедур, которые к тому же не всегда приводят к практически значимым результатам. При этом устойчивые закономерности могут быть выявлены при изучении совокупностей однородных явлений.
Уровень стохастичности аспектов деятельности организации зависит от этапа её жизненного цикла. Те стадии, которые принято называть стадиями зрелости и стабильности (модели Липпита и Шмидта, Каца и Канна, Фламхольца), обычно характеризуются большей определённостью, то есть снижением информационной энтропии за счёт формализации управления, совершенствования организационной структуры на основе адаптационных механизмов, институционального характера взаимоотношений с внешней средой [3]. Для других этапов характерны более высокие значения информационной энтропии, что увеличивает риск при принятии решений.
Другим важнейшим аспектом ЖЦО является внезапность трансформаций организационной системы из-за скрытых или плохо наблюдаемых изменений. В ряде случаев при кажущейся целенаправленности и полной управляемости бизнес-процессов менеджменту приходится сталкиваться с неопределённостью знания об особенностях взаимосвязей между элементами организационной системы, уровне их синергии и динамике изменений. Случайность и, как следствие, высокая информационная неопределённость инкрементальных структурных и процессных изменений характерна для большинства современных рыночных организаций. При этом скрытость влечёт за собой скачкообразный характер последующих, нередко радикальных, изменений.
В конечном счёте большинство изменений внутренних характеристик организации зависит от интенсивности воздействий на неё факторов внешней среды.
Накопление малозаметных изменений и перерастание их в радикальные трансформации характеризует развитие кризисов в организации на каждом из этапов её жизненного цикла [8]. Так, например, на стадии становления (модели Липпита и Шмидта, Скотта, Грейнера, Торберта [3]), когда основной целью организации является создание продукта и выживание на рынке, основным источником развития является предпринимательский потенциал собственника. На этой стадии в организации, как правило, низок уровень формализации управленческих процессов, что улучшает её деятельность. Рост организации, увеличение численности персонала и спектра решаемых задач, отсутствие инструкций и формальных процедур увеличивает время выполнения простых операций, снижает эффективность коммуникаций, ослабляет координацию действий. Отсутствие наёмного менеджмента приводит к перегрузке предпринимателя задачами оперативного управления. Эти, порой малозаметные, проблемы способны перерасти в кризис, требующий незамедлительной формализации управления и создания системы менеджмента. Неспособность руководителя своевременно выявить малые изменения в работе организации может привести к необходимости антикризисных мер. Так плохо наблюдаемые изменения могут скачком изменить состояния и структуры организации.
Разумеется, деление жизненного цикла социоров на отдельные этапы весьма условно. Разнообразие моделей подтверждает это [3–5]. Однако возможность выявить и формально описать устойчивые характерные особенности каждого этапа имеет существенное методологическое значение: такая «разрывная» интерпретация непрерывного процесса позволяет моделировать ЖЦО в классе систем со случайной, скачкообразно изменяющейся структурой [9].
Системами со случайной скачкообразной структурой (ССС) называется особый класс стохастических динамических систем, структура которых может изменяться случайным образом в случайные моменты времени [9–11]. Смена структуры представляет процесс с конечным числом возможных состояний, изменяющихся в случайные моменты времени с определённой вероятностью.
В рамках исследования ЖЦО под структурой понимается состояние организации, характерное для исследуемого этапа её развития. Другими словами, переход организации от одного этапа жизненного цикла к другому в результате постепенных или скачкообразных изменений может рассматриваться как процесс смены структур. При этом набор структур (набор этапов ЖЦО) считается конечным и заранее известным(1).
Понятие «структура» в рамках данной модели шире понятия «организационная структура», употребляемого в традиционном смысле. В модели ССС под структурой понимается достижение организационной системой состояния динамического равновесия между внутренней и внешней средой, характеризующего данный этап её жизненного цикла.
Тезис о случайности смены структур в случайные моменты времени нисколько не противоречит основным положениям концепции жизненного цикла организации. Вывод, что для уяснения сущности каждой стадии ЖЦО необходимо понимание того, как характеристики организации изменяются во времени, а также того, что организация способна возвращаться на предшествующие стадии развития [1], подтверждает необходимость учёта вероятностной динамики этих процессов. Структурная стохастичность модели ЖЦО, образно говоря, позволяет развязать последовательность этапов, устранив необходимость жёстко определять их временные периоды, а также направления переходов. Такая интерпретация вероятностно оценивает закономерности развития организации.
Термин «скачкообразный», традиционно используемый для обозначения систем, способных изменять свою структуру за предельно малые промежутки времени, применительно к моделям ЖЦО не обязательно предполагает именно такой характер смены этапов. Слово «скачкообразность» в данном случае указывает, что плавные процессы организационных изменений рассматриваются как последовательность дискретных этапов, отличающихся между собой.
(1) Такая трактовка набора этапов в целом соответствует концепции исследования ЖЦО. Тем не менее в ряде практических задач множество структур, соответствующих этапам ЖЦО, может быть не полностью определённым априори.
Существенной особенностью описания ЖЦО в классе систем ССС является то, что вектор состояния организации, помимо набора технико-экономических и социально-психологических характеристик (континуальной части), включает номер структуры (этапа развития). В отличие, например, от математического аппарата теории массового обслуживания, не учитывающего континуальной составляющей характеристик управляемой системы, теория систем ССС позволяет решать задачи, в которых структура системы (в данном случае – этап ЖЦО) зависит от её характеристик, и наоборот, характеристики определяются этапом жизненного цикла, что в полной мере соответствует концепции ЖЦО. Поэтому в наиболее общей постановке задача оценивания состояния организации приобретает характер определения вероятности(1) обобщённого вектора, учитывающего как характеристики организации, так и этап её жизненного цикла. Необходимость вероятностного подхода к оценке общего состояния организации обусловлена тем, что на практике менеджмент обычно не может точно определить, на каком этапе жизненного цикла находится его организация. Наличие же вероятностной оценки этапа ЖЦО позволит руководству принимать адекватные решения, используя ситуационный подход к управлению.
Модель ЖЦО, построенная в классе систем ССС, не только не отрицает существующие модели, основанные на выделении классификационных признаков, но и рассматривает их в качестве первичных (базовых) инструментов исследования. Применение теории ССС для анализа ЖЦО предполагает выбор на первом этапе одной или нескольких известных моделей, основанных на системе признаков смены этапов жизненного цикла. В результате выбора первичных моделей формируются конечные множества (наборы) этапов ЖЦО.
В основе модели ЖЦО в классе систем ССС лежит теорема гипотез – формула Байеса, при этом набор этапов ЖЦО, соответствующий выбранной базовой модели, рассматривается как полная группа несовместных гипотез о равновесных состояниях организации [12].
Текущая (апостериорная на каждом шаге анализа) вероятность нахождения организации на том или ином этапе жизненного цикла ![]() определяется как вероятность соответствующей гипотезы при условии совершения заранее оговорённого контрольного (индикаторного) события r(k), выступающего в роли «обновляющего процесса»:
определяется как вероятность соответствующей гипотезы при условии совершения заранее оговорённого контрольного (индикаторного) события r(k), выступающего в роли «обновляющего процесса»:

Где k – шаг анализа ЖЦО;
![]() гипотезы о возможных этапах ЖЦО на k-м шаге анализа. Начальные (априорные) вероятности гипотез
гипотезы о возможных этапах ЖЦО на k-м шаге анализа. Начальные (априорные) вероятности гипотез ![]() считаются известными(2).
считаются известными(2).
1 Точнее, плотности вероятности.
2 На момент начала процедуры динамического анализа ЖЦО.
3 Строго говоря, байесовский подход и основанные на нём модели систем ССС позволяют рассматривать в качестве «обновляющего процесса» не только косвенные признаки конкретного этапа ЖЦО, но и данные многомерного наблюдения (измерения) континуальной составляющей состояния организации – её технико-экономических, организационных и социально-психологических характеристик. Однако такой подход представляет собой достаточно сложную задачу, причём точность выводов далеко не всегда возрастает с увеличением числа анализируемых факторов. Индикатор «обновляющего процесса» лучше и дешевле.
Индикаторное событие r(k) представляет собой некоторый признак, косвенно(3) указывающий на то, что к настоящему времени сформировалось (или формируется) равновесное состояние организационной системы, соответствующее тому или иному этапу её жизненного цикла. Индикаторные наблюдения должны осуществляться подразделениями организации, ответственными за мониторинг её состояния (жизненного цикла). Априорной характеристикой, определяющей степень достоверности результатов мониторинга, является известная вероятность ![]() показывающая, насколько точно работает «индикатор».
показывающая, насколько точно работает «индикатор».
Рассмотрим пример. При переходе организации со стадии «директивного руководства» к стадии «делегирования» (модель Грейнера [3]) процесс смены централизованной бюрократической структуры децентрализованной органической структурой является необходимым и закономерным. В большинстве случаев он недостаточно наблюдаем и управляем. Пусть конечное множество гипотез на рассматриваемом промежутке времени равно двум. ![]() гипотеза о преобладании в структуре управления организацией механистических принципов, характеризующихся, помимо всего прочего, высокой частотой согласования оперативных задач на высшем уровне управления;
гипотеза о преобладании в структуре управления организацией механистических принципов, характеризующихся, помимо всего прочего, высокой частотой согласования оперативных задач на высшем уровне управления; ![]() гипотеза об органической структуре, характеризующейся доминированием неформальных связей и значительной децентрализацией управления.
гипотеза об органической структуре, характеризующейся доминированием неформальных связей и значительной децентрализацией управления.
Допустим, что в качестве индикаторного события r(k), косвенно характеризующего состояние организации, принята частота согласований оперативных задач на высшем уровне управления. Очевидно, что высокое значение этого параметра характеризует предельную централизацию управления, косвенно указывая на механистические признаки стадии «директивного руководства». Предположим, что на каждом шаге анализа работа индикатора характеризуется следующими параметрами:

Пусть начальные вероятности нахождения организации в той или иной структуре ![]() характеризуют уверенность менеджмента в доминировании признаков стадии «директивного руководства». Допустим, что в течение контрольной единицы времени индикаторное событие r(k) не состоялось ни одного раза. Тогда апостериорная вероятность сохранения признаков централизации и бюрократизации управления (этапа «директивного руководства») станет равной(1)
характеризуют уверенность менеджмента в доминировании признаков стадии «директивного руководства». Допустим, что в течение контрольной единицы времени индикаторное событие r(k) не состоялось ни одного раза. Тогда апостериорная вероятность сохранения признаков централизации и бюрократизации управления (этапа «директивного руководства») станет равной(1)
![]() а вероятность проявления свойств децентрализации управления, то есть этапа «делегирования»,
а вероятность проявления свойств децентрализации управления, то есть этапа «делегирования», ![]()
(1) Здесь и далее для упрощения формул опущен аргумент времени k.
Таким образом, наблюдение за индикаторным событием r(k) позволило сделать вывод о снижении с 0,9 до 0,71 вероятности того, что организация находится на стадии s1 – «директивного руководства», и увеличении с 0,1 до 0,29 вероятности стадии «делегирования».
В том случае, если за время контрольного периода состоится хотя бы одно согласование оперативных задач на высшем уровне управления (r(k) = 1), вероятности стадий ЖЦО примут значения![]() подтвердив предположение о доминировании признаков централизации (увеличение с 0,9 до 0,97). Следовательно, организация на стадии «директивного руководства».
подтвердив предположение о доминировании признаков централизации (увеличение с 0,9 до 0,97). Следовательно, организация на стадии «директивного руководства».
Полученные результаты отражают динамику организационных изменений на базе выбранной первичной модели ЖЦО (в примере – модель Грейнера [3]). При этом значения апостериорных вероятностей гипотез содержательно могут интерпретироваться как «доли» преобладания в организационной структуре принципов бюрократического и адаптивного управления.
Методология теории систем ССС позволяет расширить байесовскую модель за счёт дополнительного параметра – условной вероятности переходов(1), – указывающего, что у менеджмента есть априорная информация о закономерностях смены этапов жизненного цикла в соответствии с выбранной системой признаков. Так, например, условная вероятность ![]() есть заранее известная менеджменту вероятность перехода организации на этап № 2 при условии, что в настоящий момент она находится на этапе № 1. Очевидно, что вероятности переходов – не что иное, как формальное отражение знаний, опыта и интуиции руководителя (исследователя)(2).
есть заранее известная менеджменту вероятность перехода организации на этап № 2 при условии, что в настоящий момент она находится на этапе № 1. Очевидно, что вероятности переходов – не что иное, как формальное отражение знаний, опыта и интуиции руководителя (исследователя)(2).
Расширение байесовской модели за счёт использования этого параметра позволяет в полной мере учитывать предположения о закономерности смены структур. Тогда выражение для апостериорной вероятности гипотез примет вид 
вероятность продолжения первой стадии; ![]() вероятность возврата организации на первую стадию после перехода на вторую. (Апостериорная вероятность первой стадии зависит также и от вероятности возврата, если, по мнению исследователя, она не равна нулю.)
вероятность возврата организации на первую стадию после перехода на вторую. (Апостериорная вероятность первой стадии зависит также и от вероятности возврата, если, по мнению исследователя, она не равна нулю.)
На рис. 1 показаны кривые изменения вероятностей первой и второй стадий при условии, что в течение первых трёх периодов наблюдения из восьми периодов случилось индикаторное событие. На рис. 2 показаны те же кривые, но при условии, что индикаторное событие состоялось лишь в первом периоде наблюдения.
Как видно, наличие у исследователя индикаторной информации (обновляющего процесса) позволяет в реальном времени оценивать динамику изменения преобладания той или иной стадии ЖЦО.
В общем случае процедура моделирования ЖЦО должна включать следующие этапы:
(1) Термин «условная вероятность» употребляется здесь в традиционном для теории вероятностей смысле, отражая зависимость величины вероятности от выбранного условия (в данном случае – условия, что организация находится на определенном этапе жизненного цикла).
(2) В ряде случаев прикладные модели ЖЦО могут не включать вероятности переходов. Это значит, что у исследователя нет достаточных оснований предполагать закономерности смены структур.
В этом случае вероятности переходов считаются равными единице. Однако в большинстве случаев у менеджмента организации имеются вполне обоснованные предположения о некоторых переходах, основанные, например, на данных независимых организаций.

Выбор базовой модели и определение набора стадий ЖЦО.
Оценка априорной вероятности первой из анализируемых стадий.
Оценки условных вероятностей переходов на основе имеющегося опыта.
Обоснование содержания индикаторных событий для каждой из граничащих пар стадий ЖЦО.
Вероятностное описание точности работы системы мониторинга, фиксирующей индикаторные события.
Оценивание апостериорных условных вероятностей стадий ЖЦО в реальном времени по результатам наблюдений за индикаторными событиями.
На рис. 3 в качестве примера показаны графики изменения апостериорных условных вероятностей Ps1, Ps2, Ps3, Ps4 стадий ЖЦО, полученные на основе четырёхэтапной модели ЖЦО. Участки максимума вероятностей соответствуют максимальной степени уверенности менеджмента о нахождении организации в той или иной стадии.
Точки начала спада вероятностей указывают на начало снижения признаков текущей
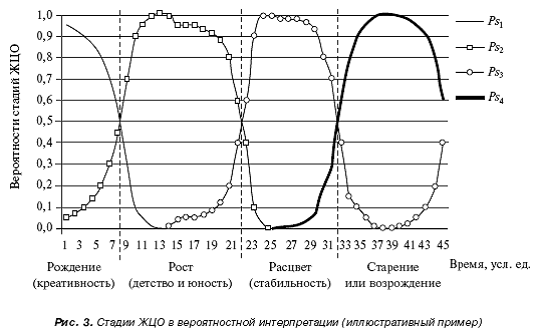
и постепенном нарастании признаков следующей стадии. Очевидно, что точки равной вероятности двух соседних стадий могут служить условным ориентиром их границ.
Для иллюстрации особого случая на рис. 3 показано снижение вероятности Ps4 четвёртой стадии, сопровождающееся возрастанием вероятности Ps3 = 1 – Ps4 третьей стадии, что указывает на появление признаков возврата организации на предыдущую стадию развития. Если в базовой модели ЖЦО четвёртая стадия соответствует фазе упадка, то возврат к фазе стабильности, очевидно, хорошая тенденция.
Определение вероятности нахождения организации на известном этапе жизненного цикла, помимо самостоятельного значения, имеет ещё и обеспечивающую роль.
Оно позволяет уточнить оценки плохо наблюдаемых переменных внутренней среды организации. Величина большинства переменных, характеризующих состояние организации, зависит от этапа её развития. Следовательно, оценка переменной должна рассматриваться как средневзвешенная по вероятностям этапов. Пусть в условиях предыдущего примера в качестве переменной x внутренней среды организации принята производительность труда персонала. Очевидно, что значение переменной x будет зависеть от типа структуры (s1 – «директивное руководство»; s2 – «делегирование»):
![]()
При известных функциях F1, F2 (где u – управленческое решение) уточнённой оценкой переменной x будет величина, зависящая от оценок вероятностей этапов ЖЦО
![]()
Таким образом, особенностью моделей ЖЦО, построенных в классе систем со случайной скачкообразной структурой, является возможность использования их для динамического анализа текущих изменений, происходящих в организации. Математический и методический аппарат данной теории, основанный на байесовском подходе к обработке информации, позволяет в реальном времени управляемых процессов оценивать вероятность каждого этапа жизненного цикла организации.
Литература
1. Широкова Г.В. Жизненный цикл организации: эмпирические исследования и теоретические подходы // Российский журнал менеджмента. – 2007. – Том 5, № 3.
2. Широкова Г.В. Теория жизненных циклов организации: анализ основных моделей // Менеджмент в России и за рубежом. – 2007. – № 2.
3. Широкова Г.В., Меркурьева И.С., Серова О.Ю. Особенности формирования жизненных циклов российских компаний (эмпирический анализ) // Российский журнал менеджмента. – 2006. – Том 4, № 3.
4. Глухова Е.В. Концепция жизненных циклов: необходимо ли понимание и применение финансистами на российском рынке? // Корпоративные финансы. – 2007. – № 4.
5. Кушелевич Е.И., Филонович С.Р. Модели жизненных циклов организаций // Менеджмент: век XX – век XXI: Сборник. – М.: Экономистъ, 2004.
6. Hanks S., Watson C., Jansen E., Chandler G. Tightening the life-cycle construct: A taxonomic study of growth stage configurations in high-technology organizations // Entrepreneurship Theory and Practice. – 1993. – № 12(2).
7. МильнерБ.З. Теория организации: Учебник. – 3-е изд. – М.: Инфра-М, 2002.
8. Дафт Р. Теория организации. – М.: Юнити, 2006.
9. Бухалев В.А. Распознавание, оценивание и управление в системах со случайной скачкообразной структурой. – М.: Наука, 1996.
10. Бухалев В.А. Оптимальное управление в системах со случайной скачкообразной структурой // Техническая кибернетика. – 1992. – № 4.
11. Казаков И.Е., Артемьев В.М., Бухалев В.А. Анализ систем случайной структуры. – М.: Наука, 1993.
12. Вентцель Е.С. Теория вероятностей: Учебник. – 9-е изд. – М.: Академия, 2003.

