Опубликовано в журнале "Финансовый менеджмент" №2 год - 2006
Мищенко А.В.,
д-р экон. наук, профессор кафедры логистики
Высшей школы экономики (ГУ-ВШЭ),
г. Москва
Чижова А.С.,
кафедра экономики и эконометрики
Университета г. Констанц, Германия
Кредитные рейтинги представляют собой оценки компаний, проранжированные и упорядоченные по убыванию вероятности дефолта, полученному кредиту либо процентным платежам по нему. Кредитный рейтинг оказывает существенное влияние на финансовую деятельность компании, поскольку не только определяет стоимость кредита, но также его доступность для компании на рынке кредитных ресурсов. Например, снижение кредитного рейтинга, с одной стороны, непременно повысит размер процентных платежей, выплачиваемых компанией по кредиту, а с другой — уменьшит количество кредитных организаций, желающих кредитовать данную компанию.
Для самих кредитующих организаций — коммерческих банков — кредитные рейтинги также являются не менее важным источником информации о финансовом состоянии. Так, например, существенную часть ежедневных операций, проводимых банками, составляют операции межбанковского кредитования (МБК<*>), связанные с размещением свободных денежных средств в банках-контрагентах. Осуществляя операции МБК, коммерческие банки выступают как в роли заемщиков, так и кредиторов других коммерческих банков, причем зачастую одновременно занимая у одних и давая в долг другим. Так как операции МБК осуществляются на короткие сроки, банкам необходимо быстро и наиболее точно оценить текущий кредитный рейтинг банка-контрагента (в случае его отсутствия) и дать его прогноз на ближайшее будущее.
<*> МБК — денежные ресурсы кредитных учреждений, размещаемые банками друг у друга в форме депозитов и на короткие сроки (от 1 дня до 6 месяцев). — Большой экономический словарь/ Под. ред. А.Н. Азрилияна. — М., 2002.
Банки, как правило, имеют более низкие, по сравнению с производственными компаниями, показатели достаточности собственных средств (капитала). В соответствии с Инструкцией ЦБ РФ № 110-И<*> минимально допустимое числовое значение норматива достаточности собственных средств для российских банков (Н1) с размером собственных средств (капитала) не менее суммы, эквивалентной 5 млн евро, составляет 10%, при этом реальные показатели достаточности капитала во многих банках близки к установленным нормативам. Данный факт объясняется стремлением банков повысить показатели доходности капитала. В такой ситуации стабильность функционирования банка во многом зависит от сложившейся рыночной репутации, отражаемой текущим кредитным рейтингом банка.
<*> Инструкция ЦБ РФ от 16 января 2004 г. № 110-И «Об обязательных нормативах банков».
Особенность кредитной истории банков состоит в том, что они являются центральным звеном финансовой системы любой страны и поэтому пользуются гораздо большей поддержкой со стороны правительственных органов (ЦБ) в случае угрозы несостоятельности (банкротства), чем производственные компании. Так, например, по данным рейтингового агентства FitchRatings<*>, вероятность дефолта производственной корпорации в среднем в четыре раза превышает вероятность дефолта банка, при том что для банка вероятность оказаться в ситуации финансовой несостоятельности и получить поддержку правительственных органов в двенадцать раз превышает аналогичный показатель для производственных корпораций.
<*> FitchRatings, Special Report 2003 «Fitch Bank Failures Study 1990—2003».
Таким образом, анализ финансовой ситуации и прогноз кредитного рейтинга банка, основанный только на оценке вероятности дефолта, не является в полной мере информативным. В связи с этим наиболее распространенный подход к оценке кредитного риска банка (JP Morgan (1997), Credit Suisse Financial Products (1997)) предполагает взаимосвязь изменений стоимости межбанковских кредитов и кредитного рейтинга занимающего банка. Вероятности изменения кредитного рейтинга банка в данном случае записываются в виде матрицы вероятностей переходов, элементами которой являются вероятности всех потенциальных изменений текущего кредитного рейтинга банка за определенный период времени.
В данной статье рассматривается модель оценки и прогнозирования долгосрочных кредитных рейтингов 61 зарубежного банка. Модель основана на показателях финансовой отчетности портфеля банков за период 2001—2003 гг. Набор данных по каждому банку включает показатели размера активов, капитала, прибыли, а также страны регистрации банка. Метод, используемый для построения модели — порядковый логит (ordered logit) — позволяет определить вероятности присвоения банку каждого из возможных кредитных рейтингов на основании показателей финансовой отчетности банка. Зависимая переменная модели — кредитные рейтинги рейтингового агентства FitchRatings, специализирующегося на присвоении рейтингов банкам и прочим кредитным организациям. В результате отбора факторов, значимых для определения кредитного рейтинга банка, выявлены следующие показатели — прибыль, достаточность капитала, прибыльность активов, прибыльность капитала и страна регистрации банка.
Структура данных
База данных, используемая при построении модели, включает наблюдения за 61 банком за период 2001—2003 гг. Таким образом, общее количество наблюдений составляет 183 банка-года. Кроме показателей размера активов, капитала и прибыли для каждого банка также определяется двоичная переменная, характеризующая страну регистрации банка, т.е.
![]()
Разделение стран на группы развитых и развивающихся осуществляется в соответствии с Инструкцией ЦБ РФ №110-И<*>.
<*> «Группа развитых стран»: Австралия, Австрийская Республика, Великое Герцогство Люксембург, Греческая Республика, Ирландия, Итальянская Республика, Канада, Королевство Бельгии, Королевство Дания, Королевство Испания, Королевство Нидерландов, Королевство Норвегия, Королевство Швеция, Новая Зеландия, Португальская Республика, Соединенное Королевство Великобритании и Северной Ирландии, Соединенные Штаты Америки, Федеративная Республика Германия, Финляндская Республика, Французская Республика, Швейцарская конфедерация, Япония.
Распределение банков по странам регистрации представлено на рис. 1.
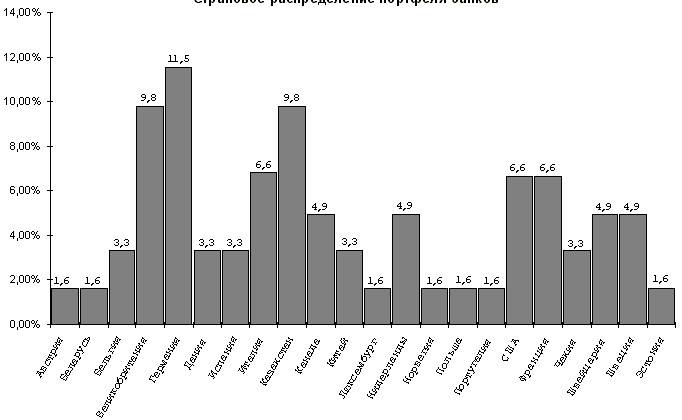
Рис.1. Территориальное распределение портфеля банков
В целях оценки текущего кредитного рейтинга банка показатели доходности капитала (ICRatio), достаточности собственных средств (капитала) (CARatio) и доходности активов (IARatio) находятся по следующим формулам:

Кредитные рейтинги, установленные рейтинговым агентством FitchRatings, изменяются в диапазоне от AAA (наивысший рейтинг) до D (дефолт)<*>. В рассматриваемом портфеле банков наиболее низкий кредитный рейтинг — ССС — присвоен белорусскому банку «Белпромстройбанк», что отражает высокую надежность банков рассматриваемого портфеля. Наиболее высокий кредитный рейтинг ААА свидетельствует об очень большой вероятности возврата размещенных на счете банка-контрагента денежных средств и процентных платежей, в то время как наиболее низкий рейтинг банков портфеля ССС свидетельствует о высокой потенциальной возможности невозврата или несвоевременного возврата размещенных денежных средств. Рейтинги в диапазоне AAA — BBB относятся к категории «инвестиционных рейтингов», рейтинги в диапазоне BB — D принадлежат категории «спекулятивных». Распределение рассматриваемого портфеля банков по кредитным рейтингам представлено на рис. 2.
<*> Определения кредитных рейтингов приводятся на сайте www.fitchratings.ru.
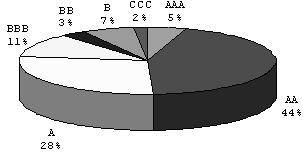
Рис. 2. Структура рейтингов кредитного портфеля
Первоначальный графический анализ распределения трех вышеуказанных показателей (CARatio, ICRatio, IARatio), показывает нелинейную, полиномиальную зависимость кредитных рейтингов от достаточности капитала, доходности активов и доходности капитала банка<*> (распределение показателя CARatio представлено на рис. 3). Данный факт может быть объяснен природой рассматриваемых показателей, каждый из которых получен как соответствующее отношение первоначальных переменных — капитала, активов и прибыли. Тем не менее, обнаруженные нелинейные зависимости не представляют сложностей для построения эконометрической модели, так как могут быть учтены посредством добавления дополнительных степенны2х объясняющих переменных: CARatio2, ICRatio2, IARatio2, CARatio3, ICRatio3,...….
<*> Здесь и в дальнейшем используется следующее цифровое соответствие кредитных рейтингов: AAA — 7, AA — 6, A — 5, BBB — 4, BB — 3, B — 2, CCC —1.
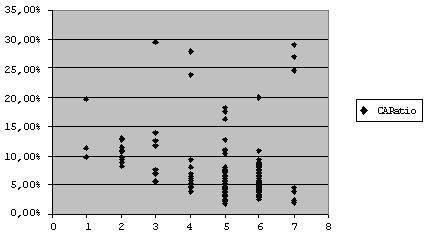
Рис. 3. Динамика показателя достаточности капитала (CARatio)
Структура модели
В основе определения кредитного рейтинга банка лежит преобразование непрерывной случайной величины, характеризующей его кредитоспособность, в дискретную, измеряемую по порядковой шкале AAA — CCC. Таким образом, каждому кредитному рейтингу банка соответствует диапазон значений его кредитоспособности. Так как кредитоспособность банка, представленная в виде кредитного рейтинга, является дискретной переменной, оценка модели с подобной зависимой переменной требует определенной модификации обычных методов.
Аналогичная ситуация складывается в случае бинарной зависимой переменной, принимающей значения {0,1}. Например, банк-резидент (1) или нерезидент (0) имеет кредитный рейтинг международных рейтинговых агентств (1) или не имеет (0). Прогнозируемые значения такой переменной должны быть непременно распределены на интервале [0;1], что позволило бы интерпретировать их как вероятности того, что зависимая переменная примет значение 1 (или 0). Моделирование бинарной переменной как линейной функции от объясняющих переменных может привести к тому, что прогнозируемые значения (вероятности) окажутся за пределами интервала [0;1]. Для избежания подобной ситуации и ограничения прогнозируемых вероятностей на интервале [0;1] используются различные симметричные распределения ошибки модели, наиболее часто используемыми из которых являются нормальное и логистическое распределения. Модель, основанная на предположении нормального распределения, получила название пробит (probit); модель, основанная на предположении логистического распределения — логит (logit). В том случае, если зависимая переменная модели может принимать более двух значений, как, например, выбор средства передвижения (автомобиль (0), поезд (1), самолет (2)), оценка вероятности того, что случайная величина примет одно из возможных значений, осуществляется с помощью моделей multinomial probit или multinomial logit, являющихся обобщениями указанных моделей.
Однако кредитные рейтинги, отражающие кредитоспособность компании (в анализируемом портфеле — банка), кроме возможности принимать более двух значений являются порядковыми переменными, т.е. большей кредитоспособности банка соответствует более высокое значение рейтинга. Соответственно, банк, имеющий кредитный рейтинг ААА, характеризуется большей кредитоспособностью, чем банк, имеющий кредитный рейтинг АА. Аналогичное утверждение, например, в отношении выбора средств передвижения совершенно не имеет смысла, поскольку данная переменная, также измеряемая по дискретной шкале, не является порядковой. Для моделирования и прогнозирования таких порядковых дискретных случайных величин, как кредитные рейтинги, используются модели, получившие названия «порядковый пробит» (ordered probit) и «порядковый логит» (ordered logit).
Данные модели основаны на предположении о том, что кредитоспособность (Y*) является линейной функцией от объясняющих переменных Х с вектором параметров ![]() <*>:
<*>:
![]()
<*> Индекс «k» относится к порядковому номеру банка, индекс «m» относится к номеру параметра модели.
Безусловно, кредитоспособность банка не является наблюдаемой переменной. Наблюдаемой переменной в данном случае является кредитный рейтинг банка, изменяющийся от ААА до ССС за период 2001—2003 гг. При этом взаимосвязь кредитоспособности банка и его кредитного рейтинга осуществляется по следующему правилу:
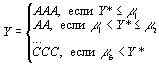
<*> В эконометрических моделях рассматриваемого вида константу модели b0 принято принимать равною нулю, b0 = 0. Данное предположение не влияет на результаты модели и позволяет оценить значение первого порогового параметра m1.
Параметры ![]() 1, ...,
1, ...,![]() 6 являются неизвестными параметрами модели, характеризующими интервалы индекса кредитоспособности, на которых банки имеют одинаковые кредитные рейтинги<*>. Эти параметры, как и вектор неизвестных параметров
6 являются неизвестными параметрами модели, характеризующими интервалы индекса кредитоспособности, на которых банки имеют одинаковые кредитные рейтинги<*>. Эти параметры, как и вектор неизвестных параметров ![]() , нуждаются в оценке в процессе оценивания модели. Оценка параметров модели, включая вектор параметров
, нуждаются в оценке в процессе оценивания модели. Оценка параметров модели, включая вектор параметров ![]() , осуществляется методом наибольшего правдоподобия. Данный метод гарантирует наилучшие асимптотические свойства оценок параметров: состоятельность и эффективность.
, осуществляется методом наибольшего правдоподобия. Данный метод гарантирует наилучшие асимптотические свойства оценок параметров: состоятельность и эффективность.
<*> В эконометрических моделях рассматриваемого вида константу модели ![]() 0 принято принимать равною нулю,
0 принято принимать равною нулю, ![]() 0 = 0. Данное предположение не влияет на результаты модели и позволяет оценить значение первого порогового параметра
0 = 0. Данное предположение не влияет на результаты модели и позволяет оценить значение первого порогового параметра ![]() 1.
1.
Модель строится на предположении о логистическом распределении ошибки модели ![]() , с математическим ожиданием 0 и параметром i = 1. Тогда искомые вероятности могут быть представлены в виде<*>:
, с математическим ожиданием 0 и параметром i = 1. Тогда искомые вероятности могут быть представлены в виде<*>:
<*> F — функция распределения вероятностей стандартного логистического распределения.

Функция максимального правдоподобия имеет следующий вид:

|
где |
|
— |
индикаторная переменная, принимающая значение 1, если банк k имеет рейтинг i, и 0 — в противном случае, т.е. |
![]()
Таким образом, параметры ![]() 1, ...,
1, ..., ![]() m и
m и ![]() 1, ...,
1, ...,![]() 6 могут быть найдены путем максимизации функции максимального правдоподобия
6 могут быть найдены путем максимизации функции максимального правдоподобия ![]()
Необходимо отметить, что влияние изменения объясняющей переменной Xj на вероятность присвоения банку кредитного рейтинга i зависит от уровня кредитного рейтинга. Например, если коэффициент ![]() j модели положителен, увеличение значения переменной Xj уменьшит вероятность присвоения банку наивысшего кредитного рейтинга AAA и увеличит вероятность присвоения наименьшего рейтинга ССС, при этом влияние на вероятности присвоения промежуточных рейтингов (AA — B) может быть как положительным, так и отрицательным.
j модели положителен, увеличение значения переменной Xj уменьшит вероятность присвоения банку наивысшего кредитного рейтинга AAA и увеличит вероятность присвоения наименьшего рейтинга ССС, при этом влияние на вероятности присвоения промежуточных рейтингов (AA — B) может быть как положительным, так и отрицательным.
Существенное отличие рассматриваемой модели от стандартных линейных эконометрических моделей заключается в том, что оценки ![]() -коэффициентов модели не равны изменениям вероятностей присвоения определенного кредитного рейтинга при единичном изменении соответствующих переменных X, т.е. не являются частными производными оцененных вероятностей
-коэффициентов модели не равны изменениям вероятностей присвоения определенного кредитного рейтинга при единичном изменении соответствующих переменных X, т.е. не являются частными производными оцененных вероятностей ![]() по переменным Xj. Более точно, изменения вероятностей, т.е. частные производные оцененных вероятностей по переменным Xj, являются функциями не только коэффициентов
по переменным Xj. Более точно, изменения вероятностей, т.е. частные производные оцененных вероятностей по переменным Xj, являются функциями не только коэффициентов ![]() , но и плотности логистического распределения, оцененного при X = Xk. Например, частная производная оцененной вероятности
, но и плотности логистического распределения, оцененного при X = Xk. Например, частная производная оцененной вероятности ![]() по переменной Xj, показывающая изменение вероятности присвоения банку k кредитного рейтинга AA при изменении показателя финансового состояния банка Xj, находится по следующей формуле:
по переменной Xj, показывающая изменение вероятности присвоения банку k кредитного рейтинга AA при изменении показателя финансового состояния банка Xj, находится по следующей формуле:
![]()
где f — плотность распределения стандартного логистического распределения.
В случае, если переменная Xj является двоичной переменной, как, например, страна регистрации банка, изменение вероятности присвоения банку k кредитного рейтинга AA при изменении переменной Xj находится по следующей формуле:
![]()
Оценка модели
Для построения модели использовались данные о 61 банке-нерезиденте<*> за период 2001—2003 гг., что составило 183 наблюдения за весь наблюдаемый период. На основании данных финансовой отчетности банков-нерезидентов на конец отчетного года в процессе оценки модели были выявлены следующие значимые показатели: чистая прибыль (Income), доходность капитала (ICRatio), доходность активов (IARatio), достаточность капитала (CARatio) и страна регистрации банка (Country). Таким образом, итоговая модель, отобранная на основании таких показателей качества модели, как псевдо-R2 и N (количество правильно прогнозируемых рейтингов), имеет вид:

где k — порядковый номер банка.
<*> Банк-нерезидент — кредитная организация, созданная и признанная банком по законодательству иностранного государства, которое является местом его регистрации.
Оценка модели осуществлялась в программном пакете EViews методом Ordered choice. Результаты оценки приведены в табл. 1.
Таблица 1
Результат оценки модели Ordered logit
|
Dependent Variable: RATING |
||||
|
Method: ML — Ordered Logit |
||||
|
Included observations: 183 |
||||
|
Number of ordered indicator values: 7 |
||||
|
|
Coefficient |
Std. Error |
z-Statistic |
Prob. |
|
INCOME |
0,000811 |
0,000181 |
4,475786 |
0,0000 |
|
(INCOME/CAPITAL)^2 |
61,87437 |
16,06497 |
3,851508 |
0,0001 |
|
(INCOME/CAPITAL)^3 |
–85,83804 |
27,65208 |
–3,104217 |
0,0019 |
|
(INCOME/ASSETS)^2 |
–5414,031 |
1573,775 |
–3,440155 |
0,0006 |
|
(INCOME/ASSETS)^3 |
59 723,31 |
22 748,49 |
2,625375 |
0,0087 |
|
(CAPITAL/ASSETS)^2 |
64,15761 |
15,14649 |
4,235806 |
0,0000 |
|
COUNTRY |
5,646535 |
0,761674 |
7,413326 |
0,0000 |
|
|
Limit Points |
|||
|
LIMIT_2:C(8) |
–1,820452 |
0,658844 |
–2,763101 |
0,0057 |
|
LIMIT_3:C(9) |
0,160613 |
0,412524 |
0,389341 |
0,6970 |
|
LIMIT_4:C(10) |
0,895598 |
0,397108 |
2,255302 |
0,0241 |
|
LIMIT_5:C(11) |
2,853114 |
0,518522 |
5,502397 |
0,0000 |
|
LIMIT_6:C(12) |
6,567284 |
0,805529 |
8,152757 |
0,0000 |
|
LIMIT_7:C(13) |
11,13264 |
1,03868 |
10,71806 |
0,0000 |
|
Akaike info criterion |
1,992022 |
Schwarz criterion |
|
2,220019 |
|
Log likelihood |
–169,2700 |
Hannan-Quinn criter. |
|
2,084440 |
|
Restr. log likelihood |
–265,0436 |
Avg. log likelihood |
|
–0,924973 |
|
LR statistic (7 df) |
191,5471 |
LR index (Pseudo-R2) |
|
0,361350 |
|
Probability(LR stat) |
0,000000 |
|
|
|
Как следует из табл. 1, показатель псевдо-R2 равен 0,36, что характеризует хорошее качество модели, учитывая небольшое количество используемых наблюдений. Показатель N — количество правильно прогнозируемых рейтингов — может быть найден на основании данных из табл. 2.
![]()
Таблица 2
Оценка качества прогнозирования по модели
|
Кредитный рейтинг |
Количество банков |
Правильно прогнозируемое количество банков |
Ошибка прогноза n |
|
AAA |
8 |
1 |
7 |
|
AA |
82 |
69 |
13 |
|
A |
54 |
24 |
30 |
|
BBB |
17 |
12 |
5 |
|
BB |
7 |
0,00 |
7,00 |
|
B |
12 |
1 |
11 |
|
CCC |
3 |
0 |
3 |
|
Итого: |
183 |
107 |
76 |
Анализ влияния используемых факторов затруднен нелинейностью модели, тем не менее в данном случае графический анализ может оказаться полезным. На рис. 4—5 представлено распределение вероятностей всех кредитных рейтингов в выборке банков в зависимости от показателя достаточности капитала (CARatio). При этом все остальные переменные приравнены к своим средним значениям:

Влияние показателя достаточности капитала на кредитный рейтинг банка
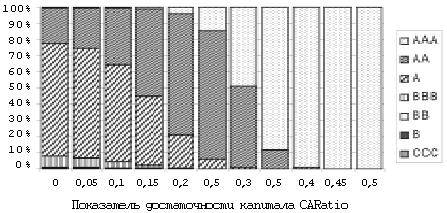
Рис. 4. Изменение кредитного рейтинга банка в зависимости от показателя достаточности капитала (CARatio)
Графический анализ, представленный на рис. 5, показывает, что для банка, обладающего вышеуказанными средними характеристиками, вероятность присвоения кредитного рейтинга АА будет максимальной при показателе достаточности капитала CARatio на промежутке [0,14; 0,3]. Данный факт отражает склонность банков придерживаться установленного норматива минимального значения достаточности капитала 10—15% в зависимости от размера банка и страны его регистрации. Рис. 5 также показывает положительное влияние переменной CARatio на кредитный рейтинг банка.
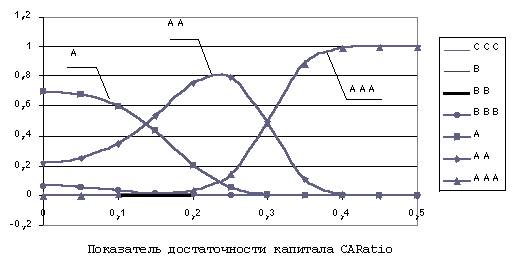
Рис. 5. Влияние показателя достаточности капитала (CARatio) на прогнозируемый уровень кредитного рейтинга банка
Рис. 6 показывает зависимость кредитного рейтинга от бинарной переменной страны регистрации банка (Country). Очевидно смещение распределения в сторону более высоких кредитных рейтингов для банков, зарегистрированных в развитых странах. При одинаковых финансовых показателях, зафиксированных на уровне выборочных средних ![]() , банк, зарегистрированный в одной из ряда развитых стран, наиболее вероятно получит кредитный рейтинг AA, в то время как банк, зарегистрированный в одной из развивающихся стран, — BBB.
, банк, зарегистрированный в одной из ряда развитых стран, наиболее вероятно получит кредитный рейтинг AA, в то время как банк, зарегистрированный в одной из развивающихся стран, — BBB.
Влияние страны регистрации (Country) на уровень кредитного рейтинга
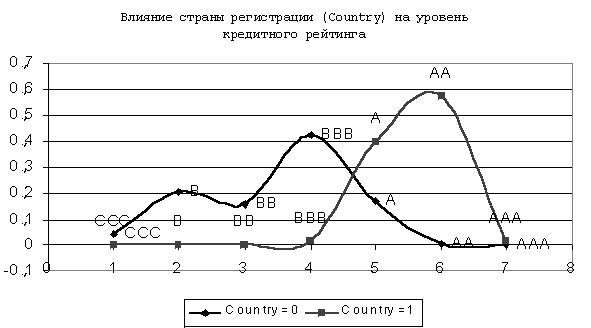
Рис.6. Сравнение распределения вероятностей присвоения кредитных рейтингов банкам развитых и развивающихся стран
Прогнозирование на основе модели
Прогнозирование по модели «порядковый логит» осуществляется на основании категории, обладающей наибольшей вероятностью. То есть прогнозируемый кредитный рейтинг банка — это кредитный рейтинг с максимальной вероятностью. В соответствии с ранее полученным результатом, показатель N модели — количество правильно прогнозируемых рейтингов — составил 58,5%. Тем не менее, по ряду кредитных рейтингов прогнозная сила модели превышает данный показатель, например, количество правильно прогнозируемых рейтингов в категории AA составило 84,1%, в категории BBB — 70,6% (табл. 3). Данный факт объясняется смещением распределения банков в рассматриваемом портфеле в сторону этих категорий, в частности категория AA составляет 44% портфеля.
Количество правильно прогнозируемых рейтингов среди 30 крупнейших банков (по размеру активов) составило 73,3%, среди 30 наиболее мелких банков — 36,6%, что показывает большую мощность прогноза в отношении крупных банков. Количество правильно прогнозируемых рейтингов среди банков развитых стран составило 66,6%, среди банков развивающихся стран — 31,0%, что также объясняется смещением распределения рассматриваемого портфеля банков в сторону банков развитых стран (77,0% портфеля).
Таблица 3
Качество прогноза модели в зависимости от категории кредитного рейтинга
|
Кредитный рейтинг |
Количество банков |
Правильно прогнозируемое количество банков |
Правильно прогнозируемое количество банков (%) |
Ошибка прогноза ni |
|
AAA |
8 |
1 |
12,5 |
7 |
|
AA |
82 |
69 |
84,1 |
13 |
|
A |
54 |
24 |
44,4 |
30 |
|
BBB |
17 |
12 |
70,60 |
5,00 |
|
BB |
7 |
0 |
0 |
7 |
|
B |
12 |
1 |
8,3 |
11 |
|
CCC |
3 |
0 |
0 |
3 |
|
Итого: |
183 |
107 |
58,5 |
76 |
Отсутствие официально присвоенных кредитных рейтингов банков-контрагентов является довольно сложной проблемой на пути оценки кредитного риска портфеля, поэтому возможность прогнозировать кредитные рейтинги банков, не имеющих официальных кредитных рейтингов, — одно из основных достоинств предлагаемой модели. В отличие от прогнозирования кредитных рейтингов в последующие периоды времени (t+1,…), требующего в качестве входных данных прогноз всех используемых в модели финансовых показателей, прогноз кредитных рейтингов банков, не имеющих официальных рейтингов, не требует дополнительной информации и основан только на текущих показателях финансовой отчетности.
В 2003—2004 гг. рейтинговое агентство FitchRatings впервые присвоило кредитные рейтинги следующим банкам: Barclays Bank Plc. (London), Vilniaus Bankas (Vilnius), Calyon Corporate and Investment Bank (Paris), J.P.Morgan Chase Bank (New York). Поскольку эти банки не имели кредитных рейтингов в 2002 г. они не были включены в выборку банков, на основании которой проводилась оценка модели. Поэтому прогноз кредитных рейтингов этих банков, приведенный в табл. 4, является прогнозом вне выборки. Примечательно то, что ошибка прогноза по этим банкам составляет не более одной кредитной категории.
Таблица 4
Сравнение прогнозируемых по модели и присвоенных кредитных рейтингов
|
Название банка (страна регистрации) |
Активы (млн долл. США) |
Капитал (млн долл. США) |
Прибыль (млн долл. США) |
Кредитный рейтинг (год присвоения) |
Прогнозируемый кредитный рейтинг |
|
Barclays Bank Plc., London (Великобритания) |
776,721 |
29,75 |
4,942 |
AA (2004) |
AA |
|
Vilniaus Bankas, Vilnius (Литва) |
3,105 |
342 |
48 |
A (2004) |
BBB |
|
Calyon Corporate and Investment Bank, Paris (Франция) |
215,812 |
5,567 |
736 |
AA (2004) |
AA |
|
J.P.Morgan Chase Bank, New York (США) |
622,388 |
35,637 |
1,213 |
A (2003) |
AA |
Выводы
Модель «порядковый логит» (ordered logit), приведенная в данной статье, позволяет оценить существующую взаимосвязь дискретно-исчисляемых кредитных рейтингов и непрерывно-исчисляемых показателей экономической активности банковских учреждений. На основании данных финансовой отчетности 61 банка-нерезидента в ретроспективе за 3 года (2001—2003 гг.) были выявлены следующие показатели, в наибольшей мере влияющие на уровень кредитного рейтинга банка: чистая прибыль (Income), доходность капитала (ICRatio), доходность активов (IARatio), достаточность капитала (CARatio) и страна регистрации банка (Country). Необходимо отметить, что абсолютные показатели уровня активов и капитала банка не являются сколько-нибудь значимыми для определения кредитного рейтинга банка.
Рекомендуемая модель может быть успешно использована для прогнозирования кредитных рейтингов банковских учреждений и выявления наиболее значимых показателей экономической активности, а также степени их влияния на кредитный рейтинг банка. Кроме того, модель может быть использована для построения матрицы вероятностей переходов, т.е. прогнозируемых изменений кредитных рейтингов банков. Данный аналитический подход к построению матрицы вероятностей переходов позволит существенно ускорить процесс ее оценки по сравнению с наиболее часто используемым историческим подходом.

