Опубликовано в журнале "Финансовый менеджмент" №4 год - 2007
аспирант кафедры
«Банковское дело и ценные бумаги»
Байкальского государственного
университета экономики и права,
г. Иркутск
Вопрос о выборе оптимального портфеля встает перед инвестором после того, как осуществлен инвестиционный анализ обращающихся на фондовом рынке активов и определена эффективная граница Марковица всех возможных портфелей этих активов. Под оптимальным портфелем понимается наилучший по соотношению «риск-доход» портфель для инвестора, соответствующий его целям инвестирования и индивидуальной склонности к риску. То есть цели инвестирования и склонность инвестора к риску являются факторами, которые влияют на выбор им того или иного портфеля активов.
Оба фактора взаимосвязаны, потому что, как правило, инвесторы выбирают цели инвестирования, соответствующие их склонности к риску. Инвесторы с низкой склонностью к риску в большинстве своем преследуют цели получения стабильного дохода или сохранения сбережений (резервов) и не ставят задач увеличения капитала с доходностью, превосходящей среднерыночную. В то же время инвесторы с высокой склонностью к риску готовы пойти на повышенный риск, преследуя цели получения значительного роста своего капитала.
В рамках современной портфельной теории выбор оптимального по соотношению «риск-доход» портфеля осуществляется посредством определения функции полезности инвестора ![]() , где U — полезность инвестора, Е — ожидаемый инвестором доход, s — риск, измеряемый среднеквадратическим отклонением доходности [2, с. 70]) и вычисления на ее основе кривой безразличия, в точке касания которой с эффективной границей портфелей находится искомый портфель [4, с. 197]. Ключевым параметром при вычислении кривой безразличия для конкретного инвестора является склонность к риску
, где U — полезность инвестора, Е — ожидаемый инвестором доход, s — риск, измеряемый среднеквадратическим отклонением доходности [2, с. 70]) и вычисления на ее основе кривой безразличия, в точке касания которой с эффективной границей портфелей находится искомый портфель [4, с. 197]. Ключевым параметром при вычислении кривой безразличия для конкретного инвестора является склонность к риску ![]() .
.
Для решения задачи выбора оптимального портфеля ценных бумаг с учетом особенностей инвесторов и их целей инвестирования необходимо определить значения склонности к риску, которая была бы свойственна конкретному инвестору. В современной литературе подходы к определению величины этого параметра сводятся к субъективной оценке инвестора экспертом, главным образом через анкетирование и количественную оценку путем предложения респонденту на выбор нескольких портфелей с различной степенью риска и анализа выбранного портфеля [4, с. 846]. На наш взгляд, необходимо разработать методику объективного определения количественных рамок показателя склонности к риску для различных инвесторов, используя взаимосвязь доходности и риска портфелей со среднерыночными показателями, а также связь вида выбираемого портфеля с предпочтениями инвестора по соотношению его риска и доходности.
В первую очередь необходимо разделить эффективную границу портфелей по степени их риска. Для этого следует определить интервалы значений q для портфелей, различающихся степенью риска — консервативного, умеренно-агрессивного и агрессивного. Чтобы определить эти интервалы, необходимо задать критерии соответствия доходности и риска, которые бы позволили различать портфели по степени риска. Это представляется возможным сделать на основе связи параметра склонности к риску и вероятности получения убытка при инвестировании. Как известно, конечная доходность портфеля, его ожидаемая доходность, измеряемая математическим ожиданием ряда исторических доходностей, и риск, определяемый среднеквадратическим отклонением этого ряда, количественно связаны между собой через доверительные интервалы достижения определенной величины конечной доходности: в 68% случаев она попадает в интервал +/– одно стандартное отклонение от ожидаемой доходности, в 95% — +/– два стандартных отклонения, в 99% — +/– три стандартных отклонения. По нашему мнению, можно сопоставить эти доверительные интервалы со степенью рискованности портфеля. Высоконадежный, или консервативный, портфель не должен принести инвестору убытков с 99%-ной вероятностью, умеренно-агрессивный — с 95%-ной вероятностью, агрессивный портфель, как самый рискованный, не принесет убытков только с 68%-ной вероятностью.
Таким образом, необходимо определить три кривых безразличия, которые будут представлять собой графическое изображение портфелей, удовлетворяющих условию попадания их конечной доходности в неотрицательную зону с доверительными интервалами 68%, 95% и 99%. Так как кривая безразличия определяется функцией ![]() [2, с. 115], то значение
[2, с. 115], то значение ![]() , начиная с которого конечная доходность для всех портфелей, лежащих на кривой безразличия в соответствии с каждым доверительным интервалом, является неотрицательной, будет являться пороговым при переходе от одного типа портфеля к другому.
, начиная с которого конечная доходность для всех портфелей, лежащих на кривой безразличия в соответствии с каждым доверительным интервалом, является неотрицательной, будет являться пороговым при переходе от одного типа портфеля к другому.
Следует отметить, что для того, чтобы вычислить показатели доходности и риска портфелей, лежащих на кривой безразличия, в соответствии с параметром ![]() , необходимо задать начальное значение полезности инвестора U. По нашему мнению, таким значением должна быть полезность, которую может получить инвестор, не принимая на себя риск, — т. е. полезность, получаемая при вложении капитала в безрисковый актив. Так как риск безрискового актива с определенной долей условности можно считать равным 0, то полезность U в соответствии с функцией, определяющей кривую безразличия, будет равна доходности, которую дает безрисковый актив.
, необходимо задать начальное значение полезности инвестора U. По нашему мнению, таким значением должна быть полезность, которую может получить инвестор, не принимая на себя риск, — т. е. полезность, получаемая при вложении капитала в безрисковый актив. Так как риск безрискового актива с определенной долей условности можно считать равным 0, то полезность U в соответствии с функцией, определяющей кривую безразличия, будет равна доходности, которую дает безрисковый актив.
В качестве безрискового актива, как правило, используются государственные ценные бумаги. Соответственно, безрисковой ставкой доходности считается доходность к погашению по государственной ценной бумаге. Однако следует отметить, что государственная ценная бумага является строго безрисковой только в разрезе систематической составляющей риска, в то время как в процессе ее обращения на фондовом рынке она подвержена влиянию специфической составляющей риска. В связи с этим в целях определения безрисковой ставки доходности необходимо выбирать такой безрисковый актив, чтобы срок его погашения был максимально приближен к сроку окончания периода удержания портфеля. Идеальной можно считать ситуацию, когда дата погашения безрисковой ценной бумаги совпадает с датой окончания периода удержания портфеля. В этом случае доходность, зафиксированную при формировании портфеля, можно будет считать безрисковой, так как специфическая составляющая риска, так же как и систематическая, будет равна 0.
Однако следует отметить, что применение вероятностной связи конечной доходности портфеля и его риска возможно только в том случае, если распределение рядов исторических доходностей активов, входящих в портфель, подчиняется закону нормального распределения случайных величин. Поэтому необходимо проанализировать данные ряды на предмет нормальности их распределения. Так как распределение суммы нормально распределенных случайных чисел также является нормальным, то, на наш взгляд, достаточно провести анализ рядов исторической доходности основных индексов, представляющих собой рынки активов, входящих в состав инвестиционного портфеля. Такими индексами в рамках настоящего исследования, предметом которого является выбор оптимального портфеля российских облигаций и ликвидных акций, будут RTSI и RUX-Cbonds.
Таким образом, требуется проверить гипотезу о том, что исторические доходности индексов, характеризующих российский рынок облигаций и ликвидных акций, подчинены нормальному закону распределения. Такие проверки, как правило, проводятся с помощью критериев согласия, основанных на выборе определенной меры расхождения между теоретическим и эмпирическим распределениями. Одним из наиболее распространенных таких критериев является критерий Пирсона (критерий ![]() ).
).
Процедура применения критерия ![]() для проверки гипотезы о том, что исследуемая случайная величина (доходность индекса) Х имеет закон распределения F(x), состоит из пяти этапов [1, с. 199]:
для проверки гипотезы о том, что исследуемая случайная величина (доходность индекса) Х имеет закон распределения F(x), состоит из пяти этапов [1, с. 199]:
- По выборке {x1, x2, … , xn} наблюдений случайной величины Х находятся оценки неизвестных параметров предполагаемого закона распределения F(x). Для нормального закона распределения это математическое ожидание и среднеквадратическое отклонение.
- Эмпирическое распределение случайной величины преобразуется в виде точечного или интервального рядов.
- Определяются теоретические вероятности pi в предположении, что выдвигаемая гипотеза верна (для нормального распределения они вычисляются с помощью функции Лапласа).
- Вычисляются наблюдаемое и экспериментальное значения статистики критерия
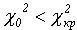
- Принимается статистическое решение: гипотеза не противоречит выборке наблюдений при заданном уровне значимости a (как правило, он обычно равен 5% или 1% [3, с. 239]), если
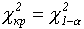 где критическая точка
где критическая точка 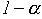 —квантиль уровня
—квантиль уровня 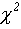 распределения
распределения 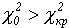 с числом степеней свободы q = k–3 (для нормального распределения, где k — количество интервалов в ряду). Если же
с числом степеней свободы q = k–3 (для нормального распределения, где k — количество интервалов в ряду). Если же 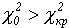 , то гипотеза отклоняется.
, то гипотеза отклоняется.
Для имеющихся рядов доходностей индексов RTSI и RUX-Cbonds критическая точка ![]() с уровнем значимости 5% составила 9,49. Произведенные вычисления показали, что для индекса RTSI
с уровнем значимости 5% составила 9,49. Произведенные вычисления показали, что для индекса RTSI![]() = 7,28, для RUX-Cbonds
= 7,28, для RUX-Cbonds ![]() = 3,01, что свидетельствует о правильности выдвинутой гипотезы. В подтверждение полученных результатов можно привести статистические характеристики исследуемых рядов данных (табл.).
= 3,01, что свидетельствует о правильности выдвинутой гипотезы. В подтверждение полученных результатов можно привести статистические характеристики исследуемых рядов данных (табл.).
Таблица
Статистические характеристики рядов исторической доходности по индексам RTSI и RUX-Cbonds
|
|
RTSI |
RUX–Cbonds |
|
Математическое ожидание |
4,52% |
1,13% |
|
Медиана |
4,67% |
1,08% |
|
Мода |
4,57% |
1,08% |
|
Асимметрия |
–0,34 |
0,12 |
|
Эксцесс |
–0,64 |
0,16 |
|
Среднеквадратическое отклонение |
8,43% |
0,90% |
Как видно из таблицы, значения математического ожидания, медианы и моды для обоих рядов данных практически совпадают, что говорит о нормальной форме закона распределения величин. Следует отметить, что наблюдается нестрогое соответствие нормальному закону распределения случайных величин, так как показатели асимметрии и эксцесса свидетельствуют о небольшом смещении ряда исторических доходностей по индексу RTSI вниз и вправо, по индексу RUX-Cbonds вверх и влево. На наш взгляд, в дальнейшем необходимо учитывать данные смещения.
Отсюда можно вывести, что гипотеза о нормальности распределения рядов исторических доходностей индексов RTSI и RUX-Cbonds подтвердилась, и применение в данном исследовании свойств закона нормального распределения случайных величин можно признать обоснованным.
Графически разделение портфелей по степени риска можно представить с помощью рисунка 1, изображающего эффективную границу Марковица и три кривых безразличия.
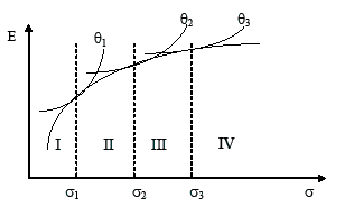
Рис. 1. Разделение эффективной границы Марковица на зоны портфелей в зависимости от склонности инвестора к риску
Кривая безразличия со склонностью к риску ![]() позволяет сделать выбор портфеля, конечная доходность которого с вероятностью 99% будет неотрицательна, при склонности к риску
позволяет сделать выбор портфеля, конечная доходность которого с вероятностью 99% будет неотрицательна, при склонности к риску ![]() конечная доходность портфеля будет неотрицательна с вероятностью 95%, при склонности
конечная доходность портфеля будет неотрицательна с вероятностью 95%, при склонности ![]() — с вероятностью 68%. Таким образом, если склонность инвестора к риску меньше, чем
— с вероятностью 68%. Таким образом, если склонность инвестора к риску меньше, чем ![]() , то его портфель будет иметь положительную конечную доходность с 99%-ной вероятностью, если она находится в интервале от
, то его портфель будет иметь положительную конечную доходность с 99%-ной вероятностью, если она находится в интервале от ![]() до
до ![]() — с 95%-ной вероятностью, при склонности к риску от
— с 95%-ной вероятностью, при склонности к риску от ![]() до
до ![]() конечная доходность портфеля будет положительна с 68%-ной вероятностью. В итоге эффективная граница Марковица разделяется на четыре зоны. Портфели, лежащие в зоне I, будут консервативными, в зоне II — умеренно-агрессивными и в зоне III — агрессивными. В зоне IV находятся портфели, конечная доходность которых окажется неотрицательной с вероятностью меньше 68%, причем данная вероятность уменьшается по мере увеличения риска. По нашему мнению, такие портфели необходимо считать сверхагрессивными и как отдельный вид добавить в классификацию портфелей по степени риска.
конечная доходность портфеля будет положительна с 68%-ной вероятностью. В итоге эффективная граница Марковица разделяется на четыре зоны. Портфели, лежащие в зоне I, будут консервативными, в зоне II — умеренно-агрессивными и в зоне III — агрессивными. В зоне IV находятся портфели, конечная доходность которых окажется неотрицательной с вероятностью меньше 68%, причем данная вероятность уменьшается по мере увеличения риска. По нашему мнению, такие портфели необходимо считать сверхагрессивными и как отдельный вид добавить в классификацию портфелей по степени риска.
Разделение эффективной границы Марковица в зависимости от склонности инвестора к риску на зоны консервативных, умеренно-агрессивных и агрессивных портфелей актуально для таких институциональных инвесторов, как профессиональные участники рынка ценных бумаг, осуществляющие деятельность по управлению негосударственными пенсионными фондами, страховыми резервами и пенсионными накоплениями. В соответствии со статьей 25, пункт 2 Федерального закона «О негосударственных пенсионных фондах» и статьей 27, пункт 2 Федерального закона «Об инвестировании средств для финансирования накопительной части трудовой пенсии в Российской Федерации» целью вложения инвестиционных ресурсов данных инвесторов является их сохранение и прирост, они не ставят перед собой задачу получения конкретной доходности по инвестиционному портфелю. То же можно отметить в отношении таких институциональных инвесторов, как страховые организации, которые при инвестировании страховых резервов также не ставят перед собой конкретные цели по достижению определенного уровня доходности: для них важно сохранить и добиться прироста резервов для обеспечения финансовой устойчивости. То есть данным институциональным инвесторам необходимо только сберечь свои инвестиционные ресурсы от их текущего обесценения (в результате инфляции), в то время как прибыль, обеспечивающая функционирование инвестора как юридического лица, извлекается посредством оказания услуг пенсионного обеспечения или страховой защиты. Поэтому, на наш взгляд, таким инвесторам будет достаточно предлагаемого разделения всего множества эффективных портфелей на указанные выше зоны и выбора оптимального портфеля по величине риска — низкой, средней и высокой — в соответствии с инвестиционной политикой. Действующая практика подтверждает правоту такой рекомендации: большинство управляющих компаний доверительного управления средствами пенсионных накоплений предлагают своим клиентам на выбор три стратегии управления: консервативную, или низкорискованную, сбалансированную и агрессивную, или высокорискованную. При управлении пенсионными резервами НПФ управляющие, как правило, используют консервативные стратегии (подтверждает это низкая доходность, полученная ими в 2005 г., по сравнению с ее среднерыночной величиной).
Вопрос выбора оптимального портфеля более актуален для доверительных управляющих, управляющих паевыми инвестиционными фондами и общими фондами банковского управления, так как они осуществляют вложение инвестиционных ресурсов уже с целью извлечения прибыли для обеспечения своей деятельности. Так как на рынке услуг доверительного управления существует потребность в различных по соотношению «риск-доход» портфелях, то для того, чтобы обеспечить спрос на свои услуги по инвестированию, таким инвесторам необходимо обладать инструментарием для обеспечения выбора оптимальных портфелей, соответствующих конкретным требованиям по величине предполагаемого дохода и риску его получения. Учитывая тот факт, что инвесторы, как правило, в первую очередь ориентируются на величину ожидаемого дохода, считаем, что методику выбора оптимального портфеля следует разрабатывать в соответствии с классификацией портфелей по источнику получения дохода.
В соответствии с данным признаком различают портфели дохода, роста и двойного назначения. Дифференциация портфелей в зависимости от источника дохода осуществляется на основе их связи с величиной риска. Наименее рискованными, или консервативными, портфелями (КП) являются портфели дохода, и инвестор, выбирая такой портфель, уверен в стабильности денежного потока, генерируемого портфелем; наиболее рискованными, или агрессивными (АП), — портфели роста, инвестор не ждет от такого портфеля текущих поступлений и, рассчитывая на увеличение стоимости портфеля в будущем, готов принять риск снижения его текущей стоимости. Соответственно, портфель двойного назначения, или сбалансированный портфель, является умеренно-агрессивным (У-АП), и инвестор выбирает такой портфель, желая избежать возможных потерь как от падения курсовой стоимости ценных бумаг, так и от низких дивидендных или процентных выплат, соглашаясь на среднерыночную величину риска. Таким образом, для определения отрезков эффективной границы Марковица, соответствующих портфелям роста, дохода и двойного назначения, можно применить описанный выше механизм разделения данной эффективной границы на портфели по степени риска.
Последующее разделение портфелей в зависимости от риска внутри полученных трех зон предлагается осуществить на основе идеи, впервые описанной У. Шарпом [4] и впоследствии развитой Р. Гринольдом и Р. Каном [5]. Идея заключается в установлении связи между доходностью и риском для равновесного рынка. Эти авторы аналитически показали, что систематическая составляющая риска тесно связана с общим риском рынка в целом, а оставшаяся часть риска должна устраняться путем выбора оптимального портфеля. Причем, если уровень риска по портфелю в целом соответствует уровню риска по всему рынку, то можно считать, что данный портфель является рыночным и имеет среднюю степень рискованности. Если инвестору необходим консервативный портфель, то оптимальным для него будет портфель с величиной риска меньше среднерыночного. Соответственно, риск агрессивного портфеля должен быть выше среднерыночного. Учитывая тот факт, что между риском и ожидаемой доходностью существует прямая зависимость (что также аналитически показано представленными выше авторами), а между конечной и ожидаемой доходностью существует вероятностная зависимость, а также то, что функционально осуществить расчет среднерыночной ожидаемой доходности значительно легче, чем расчет риска, и инвестору интуитивно проще воспринимать и анализировать показатель доходности, для определения оптимального для инвестора портфеля предлагается соотносить значения ожидаемой среднерыночной доходности (Em) и нижнего предела конечной доходности портфеля (rp). Выбор нижнего предела конечной доходности вместо ожидаемой доходности портфеля объясняется тем, что, как было показано выше, распределение исторических доходностей не является строго симметричным, и, на наш взгляд, для большей достоверности необходимо в качестве ориентира по ожидаемой доходности брать не математическое ожидание доходности, а ее нижний предел в соответствии со свойствами нормального распределения случайных величин.
Таким образом, из рисунка 2 видно последующее разделение портфелей в зависимости от риска внутри уже имеющихся трех зон: если rp <= Em, то этот портфель является консервативным, при rp = Em портфель умеренно-агрессивный, или сбалансированный, и при rp >= Em портфель агрессивный. Следует отметить, что нижний предел конечной доходности рассчитывается в соответствии с вероятностью попадания конечной доходности портфеля в неотрицательную зону для каждого из видов портфелей.
Таким образом, в рамках каждого из видов портфелей можно осуществлять выбор оптимального портфеля в соответствии с пожеланиями инвестора, ориентируясь на соотношение ожидаемой среднерыночной доходности и нижнего предела конечной доходности портфеля. Так, если инвестор в соответствии со своими предпочтениями в инвестировании хочет выбрать оптимальный портфель консервативного роста, то ему необходимо выбрать портфель, лежащий на эффективной границе Марковица в зоне с вероятностью получения неотрицательной конечной доходности портфеля 68%, причем нижний предел конечной доходности должен быть меньше среднерыночной ожидаемой доходности, рассчитанной на основе исторических доходностей индексов, характеризующих рынки ценных бумаг, входящих в искомый портфель.
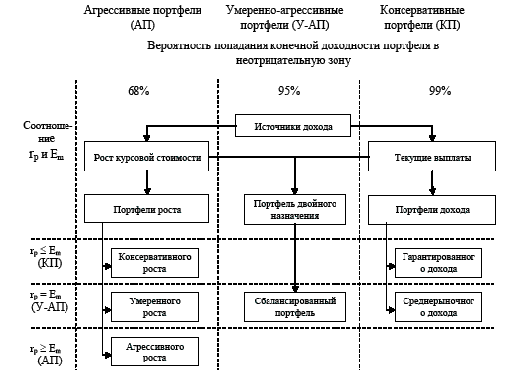
Рис. 2. Разделение портфелей (по источнику дохода) по степени риска взависимости от вероятности попадания конечной доходности портфеля внеотрицательную зону и ее соотношения со среднерыночной доходностью.
ЛИТЕРАТУРА
- Ежова Л.Н. Эконометрика. Начальный курс с основами теории вероятностей и математической статистики. Иркутск: Изд-во БГУЭП, 2002.
- Касимов Ю.Ф. Введение в теорию оптимального портфеля ценных бумаг. М.: «Анкил», 2005.
- Уотшем Т. Дж., Паррамоу К. Количественные методы в финансах: Пер. с англ. под ред. М. Р. Ефимовой. М.: Финансы, ЮНИТИ, 1999.
- Шарп У.Ф., Александер Г.Д., Бэйли Д.В. Инвестиции. Investments. М.: ИНФРА-М, 2003.
- Grinold R. C., Kahn R.N. Active portfolio management: a quantitative approach for providing superior returns and controlling risk / 2nd ed. New York: McGraw-Hill, 1999.
- http://www.cbonds.info/ru/rus/index/
- http://www.finam.ru/analysis/export/default.asp.

