Опубликовано в журнале "Маркетинг в России и за рубежом" №4 год - 2011
Булгаков Ю.В.,
доцент кафедры менеджмента
Красноярского государственного
аграрного университета
Стратегические прогнозы на основе сложившихся тенденций почти никогда не сбываются в реальности.
Для прогнозирования объемов продаж и запасов чаще всего используют методы скользящей средней, экспоненциального сглаживания, Холта, Холта–Винтера, ARIMA (АРПСС – авторегрессия проинтегрированного скользящего среднего). Все они, в том числе и нейронные сети, реализованы в системе Statistica и многих других программных продуктах. Выбор метода зависит, в первую очередь, от поставленной цели, характера и параметров временного ряда.
В данной статье в качестве альтернативы предлагаются динамические адаптивные модели для планирования запасов и продаж, реализованные в системе Matlab/Simulink [2]. Теоретические основы методов прогнозирования временных рядов не рассматриваются, поскольку они имеются в справочниках и учебниках по статистике, а также широко представлены в Интернете.
Хотя все перечисленные модели относятся к адаптивным в том смысле, что учитывают текущую информацию, предлагаемые модели позволяют получить решение при оптимальных значениях весовых коэффициентов, соответствующих наилучшему качеству аппроксимации. Под аппроксимацией понимается сглаживание фактического временного ряда расчетной траекторией, предназначенной для прогнозирования следующего значения показателя. Наиболее распространенным критерием выбора оптимального варианта в теории и практике управления является минимум среднего квадрата ошибки, то есть из каждого фактического значения вычитают соответствующие расчетные величины, возводят разницу в квадрат и находят среднее значение. При этом получаются довольно большие или, наоборот, очень малые числа, поэтому из полученного результата извлекают квадратный корень и получают абсолютную среднеквадратическую ошибку RMS (roots-mean-square). Относительную среднеквадратическую ошибку получают на основе отношения абсолютной текущей ошибки к фактическому значению.
Кроме этого критерия используют и другие, полученные в виде средних абсолютных или относительных погрешностей прогноза, причем разные критерии часто приводят к разным результатам. В данной работе для выбора варианта решения используется критерий RMS.
В качестве исходных данных использован динамический ряд квартальных продаж продукции предприятия за предшествующие шесть лет, то есть ряд включает 24 наблюдения. На рис. 1 показана модель прогнозирования на следующий квартал методом скользящего среднего с двумя (Mean) и тремя наблюдениями (Mean1) в интервале-окне для расчета текущей средней.

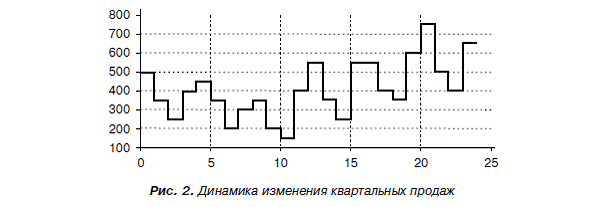
Модель дискретная с шагом один квартал, время моделирования равно числу наблюдений плюс единица для всех моделей, но поскольку отсчет времени начинается с нуля, модельное время задается 24. На схеме блок From Workspace принимает вектор s фактических значений для соответствующих моментов времени t из рабочей области, куда он в свою очередь поступает из Excel. Этот вектор отображается на экране осциллографа Scope, показанном на рис. 2, где горизонтальная ось времени соответствует номеру квартала, а вертикальная – объему продаж в натуральном измерении.
В данном случае анализируется один временной ряд, но одновременно в блок From Workspace можно передавать из электронных таблиц и обрабатывать данные для сотен наименований товаров.
Блоки Tapped Delay используются для получения сглаживающего окна. Каждый из них формирует из одного вектора исходных данных соответственно два или три вектора, которые сдвинуты на один шаг относительно друг друга. Скользящие средние вычисляют блоки Mean и Mean1, а результаты выводятся на дисплеи 1 и 2, которые и являются прогнозом. Далее результаты с помощью мультиплексора Mux1 объединяются для уменьшения размеров блок-схемы, а в блоке Add, который предназначен для алгебраического сложения, выполняется их поэлементное вычитание из фактических данных. Для расчета относительной ошибки служит блок Divide, который выполняет поэлементное деление абсолютного отклонения на фактические значения.
Блок Mux2 вновь объединяет результаты вычислений с той же целью – сделать схему более компактной. Блок RMS вычисляет среднеквадратическую относительную и абсолютную ошибки для обоих вариантов, которые отображаются на дисплее 3. Блок simout предназначен для передачи обработанной информации в рабочую область и при необходимости – в таблицы Excel. Видно, что несколько меньшую ошибку имеет модель скользящего среднего с тремя наблюдениями в окне. Абсолютные и относительные среднеквадратические ошибки, как показывает дисплей 3 на рис. 1, составляют 173,05/0,49 для варианта с двумя наблюдениями и 152,64/0,45 – для варианта с тремя наблюдениями в окне.
Другой вариант этой же модели с использованием дискретного фильтра при тех же исходных данных показан на рис. 3. В блоках Discrete FIR Filter1,2 записаны формулы для вычисления скользящих средних, а блоки Integer Delau1,2 выполняют сдвиг вектора расчетных величин на один шаг модельного времени при начальном значении, равном начальному уровню исходного ряда.

Модели экспоненциального сглаживания (рис. 4) и все остальные рассмотренные модели основаны на рекурсивных формулах, когда на каждом шаге расчета
используются результаты вычислений, полученные на предыдущем шаге. Поэтому всегда существует проблема выбора начальных условий, иначе алгоритм не будет работать. Для простого экспоненциального сглаживания в качестве начального значения теоретического ряда обычно принимают фактический начальный уровень. Каждое новое предсказанное значение определяется как средневзвешенное двух предыдущих значений (фактического и теоретического) с весами ![]() и (1 –
и (1 – ![]() ) соответственно. Однако величина весовых коэффициентов, как правило, выбирается либо произвольно, либо методом проб и ошибок.
) соответственно. Однако величина весовых коэффициентов, как правило, выбирается либо произвольно, либо методом проб и ошибок.
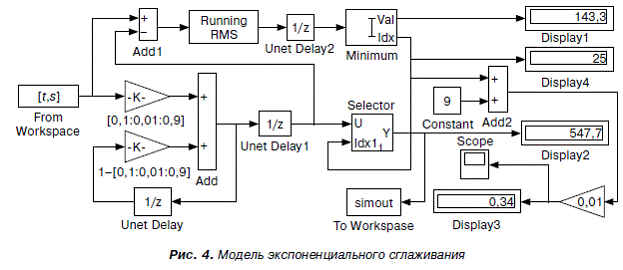
В блочной модели, приведенной на рис. 4, выполняется имитационное моделирование при различных значениях альфа. Для этого в первом блоке-умножителе заданы значения ![]() с 0,1 до 0,9 с шагом 0,01, как показано на схеме, а в другом – соответствующее дополнение до единицы, что позволяет получить 81 вариант сглаженного ряда. Блоки задержки Unit Delay обеспечивают синхронизацию процесса моделирования, а начальные значения для них устанавливаются исходя из логических соображений.
с 0,1 до 0,9 с шагом 0,01, как показано на схеме, а в другом – соответствующее дополнение до единицы, что позволяет получить 81 вариант сглаженного ряда. Блоки задержки Unit Delay обеспечивают синхронизацию процесса моделирования, а начальные значения для них устанавливаются исходя из логических соображений.
При запуске модели блок Minimum находит минимальное значение среднеквадратической ошибки и соответствующий номер варианта (дисплеи 1 и 4), а блок Selector выводит на дисплей 2 прогноз продаж на следующий период. Видно, что оптимальным вариантом является 25 (дисплей 4), то есть наилучшее качество сглаживания фактического ряда динамики обеспечивается при ![]() равном 0,34 (номер варианта плюс девять, разделить на сто – дисплей 3). При необходимости можно уменьшить интервал дискретизации для коэффициента
равном 0,34 (номер варианта плюс девять, разделить на сто – дисплей 3). При необходимости можно уменьшить интервал дискретизации для коэффициента ![]() до сколь угодно малой величины. Таким образом, отпадает необходимость поиска приемлемых значений альфа.
до сколь угодно малой величины. Таким образом, отпадает необходимость поиска приемлемых значений альфа.
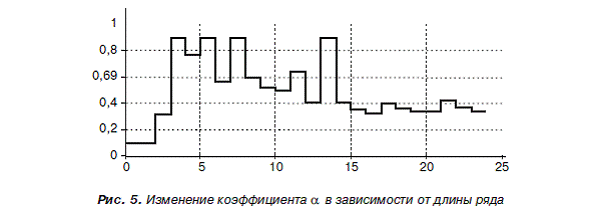
Следует отметить еще одно важное преимущество рассмотренной динамической модели. При поступлении новых данных коэффициент ![]() изменяется, адаптируя сглаженные данные к новой ситуации, а во всех известных методах этот коэффициент является заранее заданной величиной. На рис. 5 показана зависимость коэффициента
изменяется, адаптируя сглаженные данные к новой ситуации, а во всех известных методах этот коэффициент является заранее заданной величиной. На рис. 5 показана зависимость коэффициента ![]() на вертикальной оси от номера наблюдения (горизонтальная ось), полученная с осциллографа Scope.
на вертикальной оси от номера наблюдения (горизонтальная ось), полученная с осциллографа Scope.
В принципе нас не интересуют конкретные значения ![]() а также других коэффициентов, используемых в моделях прогнозирования. Практический интерес представляет лишь количественная оценка прогноза и его примерная точность. Поэтому для контроля результатов в блоках-умножителях, которые имеют форму треугольника, использовались равномерно распределенные в интервале [0,1] случайные числа.
а также других коэффициентов, используемых в моделях прогнозирования. Практический интерес представляет лишь количественная оценка прогноза и его примерная точность. Поэтому для контроля результатов в блоках-умножителях, которые имеют форму треугольника, использовались равномерно распределенные в интервале [0,1] случайные числа.
В один из этих двух блоков вводится формула 0,1 + 0,8 ? rand (10000,1), а во второй – дополнение до единицы, то есть получается столбец из десяти тысяч случайных коэффициентов ![]() и соответственно столько же вариантов расчетного ряда динамики. При этом получаются практически такие же конечные результаты.
и соответственно столько же вариантов расчетного ряда динамики. При этом получаются практически такие же конечные результаты.
Модель Холта отличается от простого экспоненциального сглаживания тем, что учитывает так называемый локальный тренд, то есть изменение цепных абсолютных приростов во времени. С этой целью кроме параметра ![]() вводится новый параметр экспоненциального сглаживания
вводится новый параметр экспоненциального сглаживания ![]() и соответственно (1 –
и соответственно (1 – ![]() ). Тогда сглаженную функцию
). Тогда сглаженную функцию ![]() рассчитывают по формуле (1):
рассчитывают по формуле (1):
![]()
где ![]() – фактический уровень ряда в момент t.
– фактический уровень ряда в момент t.
Функция ![]() учитывающая локальные тренды:
учитывающая локальные тренды:
![]()
Прогноз процесса ![]() на
на ![]() единиц вперед вычисляется по формуле
единиц вперед вычисляется по формуле
![]()
На рис. 6 показана блочная структура модели Холта.
При использовании модели Холта также возникает проблема начальных условий. Существуют различные формальные процедуры их определения, которые вследствие недостаточного обоснования не дают существенного эффекта. Поэтому в данной модели, как и в предыдущей, начальный уровень расчетного ряда принят равным фактическому уровню, а начальный тренд – нулю.
Видно, что модель Холта приводит даже к большей ошибке по выбранному критерию (дисплей 1), чем оптимальное однопараметрическое экспоненциальное сглаживание. Однако если за начальный уровень сглаженного ряда принять среднее значение за первые четыре квартала (375, блок Uniti Delau2), а за начальный тренд – средний абсолютный прирост за период, включая первый квартал следующего года (–12,5, блок Uniti Delau3), то ошибка уменьшается до 142,6 при почти таком же прогнозе. Кроме того, результат прогнозирования в абсолютном выражении (дисплей 2) даже без изменения начальных условий ближе к фактическому значению. Для оценки начальных условий кроме приведенного способа можно найти уравнение регрессии для первых пяти-шести наблюдений, тогда отрезок (параметр смещения) принимается за начальный уровень, а наклон (угловой коэффициент) – за начальный тренд. Хотя эта операция в Excel занимает доли секунды, существенных улучшений качества прогноза она тоже не дает. В системе Statistica начальный линейный тренд для модели Холта определяется как отношение разности конечного и начального фактических уровней ряда к числу наблюдений без единицы, а начальный уровень сглаженного ряда принимается равным фактическому начальному уровню минус половина расчетного тренда.

В модели Холта–Винтера дополнительно вводится параметр ![]() для учета периодических колебаний уровней ряда (сезонности). Под сезонностью понимают периодические изменения уровней ряда любой природы, не обязательно связанные с календарем. Существуют мультипликативный и аддитивный варианты учета сезонных изменений показателя. Если амплитуда сезонных колебаний увеличивается во времени, то используют мультипликативный вариант (умножение), а если амплитуда практически не изменяется – аддитивный (сложение).
для учета периодических колебаний уровней ряда (сезонности). Под сезонностью понимают периодические изменения уровней ряда любой природы, не обязательно связанные с календарем. Существуют мультипликативный и аддитивный варианты учета сезонных изменений показателя. Если амплитуда сезонных колебаний увеличивается во времени, то используют мультипликативный вариант (умножение), а если амплитуда практически не изменяется – аддитивный (сложение).
Прогноз процесса ![]() на
на ![]() единиц вперед при линейном тренде для мультипликативного варианта [3]:
единиц вперед при линейном тренде для мультипликативного варианта [3]:
![]()
где s(t) – периодическая функция;
p – число точек ряда, наблюдаемых в течение одного периода, например, если данные собирают ежемесячно в течение годового периода, то p = 12, а если ежеквартально, то p = 4. Если в качестве периода принята неделя и данные собирают ежедневно, то p = 7.
Пересчет функций в каждый момент времени выполняется по уравнениям:
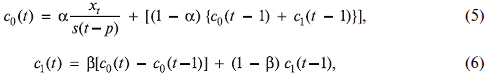
![]()
Видно, что первое уравнение (5) отличается от соответствующего уравнения в модели Холта (1) только делителем s(t – p), учитывающим эффект сезонности, второе уравнение (6) остается без изменений, однако дополнительно вводится периодическая функция s(t) с коэффициентами экспоненциального сглаживания ![]()
Формулы для аддитивного варианта отличаются от приведенных лишь тем, что вместо деления и умножения для учета сезонности используют операции вычитания и сложения.
Для получения периодической функции s(t) используется модель, приведенная на рис. 7, с помощью которой рассчитываются усредненные квартальные сезонные коэффициенты применительно к мультипликативному варианту, показанные на дисплее. Сумма коэффициентов должна быть равна длине сезонного цикла, то есть четырем.

В качестве основного используется блок Detrend, который удаляет трендовую составляющую в исходных данных. Блок Add вычисляет тренд, а в блоке Divide выполняется поэлементное деление фактических уровней ряда на сглаженные значения. Блок Reshape преобразует полученный вектор в матрицу размерности [p, k], где р – длина сезонного цикла (4), а k – число полных сезонных циклов в исходных данных (6). Блок Gain1 выполняет матричное умножение на единичную матрицу ones (k,1), которая представляет собой вектор-столбец из шести единиц.
Блоки Add1 и Divide1 выполняют сложение и поэлементное деление соответственно, а блок Gain2 – умножение на длину сезонного цикла p.
Таким образом получается периодическая функция для использования в модели Холта–Винтера; начальный уровень принимается равным фактическому, а начальный тренд – нулю, как и в предыдущих моделях. В системе Statistica начальный линейный тренд для модели Холта–Винтера определяется аналогично модели Холта, как отношение разности средних фактических уровней ряда за последний и первый периоды к произведению числа сезонных периодов без единицы на число наблюдений в одном периоде. Начальный уровень сглаженного ряда принимается равным среднему фактическому уровню за первый период минус половина расчетного тренда, умноженного на число наблюдений в одном периоде.
Следует отметить, что начальные значения влияют лишь на показатель RMS, а на результаты прогнозирования практически не влияют.
На рисунке 8 показана структура мультипликативной модели Холта–Винтера, которую можно условно разделить на три подсистемы.

Подсистема в верхней части блок-схемы является универсальной для всех моделей и предназначена для определения среднеквадратической ошибки с помощью блока RMS.
Подсистема в средней части полностью копирует модель Холта, за исключением блока Divide, который выполняет деление фактических данных на функцию s(t – p).
Подсистема в нижней части блок-схемы по существу является вкладом Винтера в модель Холта. Ключевыми здесь являются блоки Integer Delay, которые формируют сезонные волны. В блоке Integer Delay1 записан вектор [v v v v v v], где v – вектор коэффициентов сезонности, а в блоках Integer Delay2, 4 – один вектор v = [1.34 0.90 0.64 1.12]. Для получения прогнозных значений объема продаж на следующие четыре квартала используются основные блоки Delays и Gain1, 2. В блоке Gain2 записан единичный вектор-столбец ones (p, 1), а в блоке Gain1 вектор q = [1, 2, 3, 4], элементы которого соответствуют номеру квартала прогнозного периода. Оптимальные значения коэффициентов альфа, бета и гамма можно выбирать с помощью имитационного моделирования по тому же принципу, что и для простого экспоненциального сглаживания.
Учет эффекта сезонности с помощью этой модели обеспечивает примерно двукратное снижение ошибки (65,5) по сравнению с предыдущими моделями.
Кроме того, она обеспечивает и минимальную абсолютную ошибку прогноза, поскольку фактическое значение, которое не учитывалось в данных, составляет 850 ед.
На рис. 9 показана структура аддитивной модели Холта–Винтера, которая аналогична мультипликативной и, по-видимому, не требует дополнительных пояснений.

Для получения периодической функции s(t) применительно к аддитивному варианту используется модель, приведенная на рис. 10, с помощью которой рассчитываются усредненные квартальные сезонные составляющие, показанные на дисплее. Сумма сезонных составляющих в данном случае должна быть равна нулю.

Причина сравнительно высокой эффективности двух последних моделей заключается в том, что исходный ряд имеет сезонные изменения, заметные даже без дополнительного анализа (рис. 2). Видно, что в первом и четвертом кварталах объемы продаж существенно выше, чем во втором и третьем. В предыдущих моделях эффект сезонности не учитывается. Оценку периодичности временного ряда выполняют с помощью анализа автокорреляционных функций и периодограмм.
Поскольку частота и период находятся в обратной зависимости, пик на временной периодограмме для анализируемого ряда имеет период 4, а на частотной – 0,25.
Проверка всех рассмотренных моделей выполнялась сравнением полученных результатов с соответствующими расчетами в системе Statistica.
Кроме экспоненциальных моделей используются и другие методы прогнозирования временных рядов с учетом сезонных колебаний. Для определения сезонных составляющих обычно применяют метод скользящих средних, который связан с потерей части информации и довольно трудоемкими вычислениями. Поэтому в данной работе предлагаются аддитивный и мультипликативный варианты динамических моделей, основанные на удалении тренда, которые в определенном смысле имеют преимущество перед экспоненциальными моделями, поскольку не требуют эмпирических коэффициентов и обеспечивают приемлемую ошибку прогноза.
На рис. 11 показана структура мультипликативной модели, которая существенно отличается от соответствующей модели Холта–Винтера. Модельное время в данном случае равно длине ряда n плюс длина сезонного цикла p(24 + 4 = 28). Данная модель также включает три подсистемы.
Подсистема в верхней части блок-схемы предназначена для вычисления сезонных коэффициентов и почти полностью копирует схему, приведенную на рис. 7.
Добавлен лишь блок Gain3, где в качестве множителя записано выражение для единичной вектор-строки ones (1, k), где k – число полных сезонных циклов.
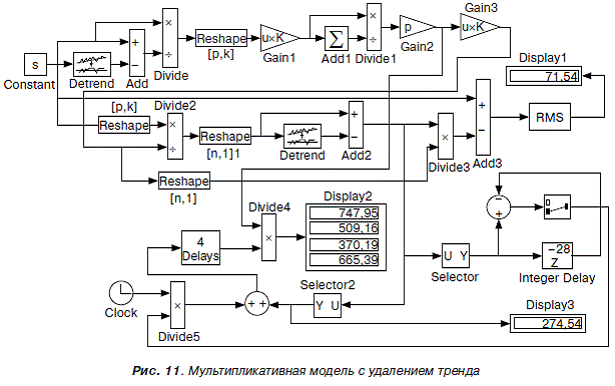
Подсистема в средней части блок-схемы предназначена для вычисления сглаженных значений уровней ряда и среднеквадратической ошибки. При этом используются блоки Reshape преобразования данных в матрицы, размерность которых показана вместо имени блока, где n = p ? k – число уровней ряда. Исходные данные s находятся в блоке Constant, то есть непосредственно не связаны со временем, поскольку иначе вычислить трендовую составляющую нельзя. Кроме исходного ряда s в рабочей области или в Excel необходимо задать значения всего трех параметров p, k и n. При этом на блоках Delays и Integer Delay автоматически появляются числа, соответствующие длине сезонного цикла и времени моделирования.
После запуска модели на дисплее Display3 появляется число, соответствующее начальному значению сглаженного ряда. Это число надо ввести в качестве начального значения в блок Integer Delay и повторно запустить модель.
Подсистема в нижней части блок-схемы предназначена для получения прогноза продаж на следующий год по кварталам. Принцип расчета заключается в том, что с помощью источника временного сигнала Clock, блоков Selector и блока Integer Delay вычисляются прогнозные значения сглаженного ряда, которые в блоке Divide умножаются на сезонные коэффициенты и выводятся на дисплей Display2. Среднеквадратическая ошибка RMS фиксируется на дисплее Display1.
На рис. 12 показана структура аддитивной модели прогнозирования, которая принципиально не отличается от мультипликативной модели и поэтому не требует отдельных комментариев.

Апробация последних моделей выполнялась по фактическим данным следующим образом. Время моделирования задается не 28, а 24, то есть на длину сезона меньше, и сравниваются показания дисплея Display2 с фактическими данными.
Ошибка в обоих случаях лежит в допустимых пределах, но несколько меньше для мультипликативной модели.
В итоговой таблице (табл. 1) показаны основные показатели эффективности рассмотренных моделей. В качестве главного критерия эффективности модели естественно считать меру соответствия прогноза фактическому значению показателя. Абсолютная ошибка представляет собой модуль отклонения расчетного значения от фактического объема продаж на следующий квартал, равного 850 ед.
Относительная ошибка определяется отношением абсолютной ошибки к известному фактическому значению. В качестве дополнительного критерия эффективности приведены значения абсолютной среднеквадратической ошибки RMS. Видно, что минимальную погрешность обеспечивает мультипликативная модель Холта–Винтера (М), хотя соответствующая аддитивная модель (А) характеризуется несколько меньшим значением RMS. Приемлемую точность обеспечивают и мультипликативная модель с удалением тренда (М), а также соответствующая аддитивная модель (А).
Первые три модели для прогнозирования данного временного ряда непригодны, поскольку имеют недопустимо высокую погрешность, верхним пределом которой в прогнозировании социально-экономических процессов обычно считается величина 20%.
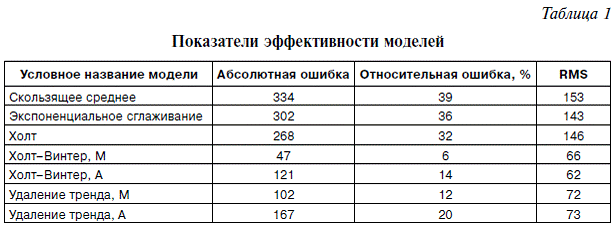
Кроме того, можно сделать вывод, что разработанные модели, основанные на удалении тренда без использования экспоненциальных коэффициентов, проще, нагляднее и вполне конкурентоспособны по эффективности в сравнении с моделью Холта–Винтера.
Основным преимуществом рассмотренных моделей по сравнению с традиционными методами являются возможность моделирования динамики любых процессов, что позволяет повысить оперативность и надежность прогноза.
Испульзуемые источники
1. Ханк Д.Э., Уичерн Д.У., Райтс А. Дж. Бизнес-прогнозирование. – 7-е изд.: пер. с англ. – М. : Вильямс, 2003.
2. Черных И.В. SIMULINK: среда создания инженерных приложений. – М. : ДИАЛОГ-МИФИ, 2003.
3. Вероятность и математическая статистика : энциклопедия / под ред. Ю.В. Прохорова. – М. : Большая Российская энциклопедия, 2003.

