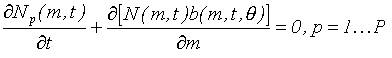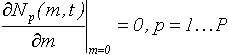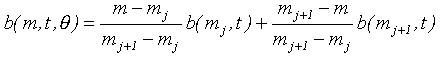Опубликовано в журнале "Финансовый менеджмент" №4 год - 2007
канд. физ.-мат. наук,
начальник управления платежных средств
ОАО «Челябинвестбанк»
Развитие российских коммерческих банков в последние годы характеризуется значительным расширением розничного бизнеса. Происходит активное наращивание сети подразделений банков, привлечение новых клиентов – физических лиц, в конкурентной борьбе создаются новые проекты по массовому перечислению заработной платы сотрудников предприятий на счета в банке. Тем самым увеличивается доля остатков на счетах физических лиц в балансе банка.
В этой связи традиционная задача прогнозирования изменения остатков на счетах клиентов – физических лиц приобретает особую значимость [1-2]. При этом важны как локальные прогнозы поведения некоторых групп клиентов, так и прогнозы изменения ресурсов банка в целом, прогнозы изменения ликвидности. Кроме того, в связи с развитием социальных программ перечисления денежных компенсаций на счета граждан задача приобретает макроэкономический аспект, связанный с прогнозированием движения денежных средств в реальном секторе экономики.
Одновременно с развитием розничных проектов происходит совершенствование информационных систем, обеспечивающих не только хранение сведений обо всех операциях клиентов, но и позволяющих формировать аналитические выборки данных по различным группам операций. Формирование таких выборок позволяет широко применять для прогнозирования статистические методы на основе реальных данных об операциях клиентов [2]. Кроме того, становится возможным применение методов социодинамики [3] и эконофизики [4], что дает возможность не только статистически «предсказать» изменение остатков на счетах клиентов, но и выявить закономерности экономических и социальных процессов, оценить влияние различных факторов на динамику движения денежных средств.
В настоящей статье предпринята попытка применения методов социодинамики [3], а также проведения аналогий с методами математического моделирования ряда физических процессов, для прогнозирования изменения остатков на банковских счетах физических лиц с учетом поведенческих особенностей различных категорий клиентов.
Математическая модель. Рассмотрим кредитную организацию, занимающуюся розничным бизнесом и имеющую значительное количество клиентов – физических лиц, на счета которых массово перечисляются денежные средства.
Будем рассматривать каждого из клиентов как элемент социодинамической системы, характеризуемой некоторой социоконфигурацией M [3]. Учитывая цели настоящего моделирования, будем считать, что состояние в системе каждого k-го клиента полностью определяется остатком на его счете mk в момент времени t, т. е. M = {m1,…, mK}, где K – количество клиентов. Изменение конфигурации M происходит за счет снятия клиентами денежных средств со скоростью b(mk,t,![]() ) (
) (![]() – переменная состояния системы), а также за счет внешнего воздействия на систему, выраженного в разовых зачислениях денежных средств клиентам F(mk, Ti) в дискретные моменты времени t = Ti (i = 1..n). При этом, поскольку количество клиентов K велико, то будем считать, что функция b(m,t,
– переменная состояния системы), а также за счет внешнего воздействия на систему, выраженного в разовых зачислениях денежных средств клиентам F(mk, Ti) в дискретные моменты времени t = Ti (i = 1..n). При этом, поскольку количество клиентов K велико, то будем считать, что функция b(m,t,![]() ) зависит только от среднестатистической суммы остатка денежных средств на счете клиента m, параметра
) зависит только от среднестатистической суммы остатка денежных средств на счете клиента m, параметра ![]() и времени t, а от поведенческих особенностей конкретного клиента не зависит.
и времени t, а от поведенческих особенностей конкретного клиента не зависит.
Таким образом, получаем систему из K элементов, определяемую конфигурацией M и изменяющуюся под внешним воздействием F. Задача исследования заключается в определении состояния конфигурации M в произвольный момент времени. Описанная в таком виде система соответствует физическим процессам фазовых переходов на этапе роста большого количества сформировавшихся кластеров в некоторой среде. Решение таких задач детально проработано [5–7]. Поэтому, развивая указанные аналогии, воспользуемся методом [7], построенным на принципе консолидации сходных по свойствам кластеров. В нашем случае будем группировать клиентов по размерам остатков денежных средств, что позволит дополнительно получить информацию о поведении различных групп клиентов.
Рассмотрим изменение во времени t количества клиентов, имеющих остаток денежных средств m. Пусть N(m,t) – такая величина, что для малого интервала ![]() денежных средств произведение N(m,t)
денежных средств произведение N(m,t)![]() равно количеству клиентов, имеющих на своих счетах остаток денежных средств в интервале от m до m+
равно количеству клиентов, имеющих на своих счетах остаток денежных средств в интервале от m до m+![]() . При этом будем считать, что количество клиентов очень велико, и величину N(m,t) можно рассматривать как непрерывную функцию.
. При этом будем считать, что количество клиентов очень велико, и величину N(m,t) можно рассматривать как непрерывную функцию.
Составим уравнение баланса функции N(m,t) в интервале от mН до mН+ ![]() (mН – начальное значение m в интервале). С одной стороны, скорость изменения количества клиентов в интервале денежных средств равно разности скорости «поступления» и «ухода» клиентов N(mН+
(mН – начальное значение m в интервале). С одной стороны, скорость изменения количества клиентов в интервале денежных средств равно разности скорости «поступления» и «ухода» клиентов N(mН+![]() ,t) b(mН+
,t) b(mН+![]() ,t,
,t,![]() ) – N(mН,t) b(mН,t,
) – N(mН,t) b(mН,t,![]() ). С другой стороны, скорость изменения количества клиентов можно представить как частную производную по времени от количества клиентов в рассматриваемом интервале
). С другой стороны, скорость изменения количества клиентов можно представить как частную производную по времени от количества клиентов в рассматриваемом интервале  Приравнивая и преобразуя выражения получаем:
Приравнивая и преобразуя выражения получаем:
|
|
(1) |
Кроме того, будем считать, что нам известны суммы разовых зачислений денежных средств клиентам в различные моменты времени.
|
|
(2) |
Для определения начальных и граничных условий предположим, что известно начальное распределение функции N(m,0)= N(m)Н. Кроме того, известно некоторое граничное значение mГ, которое превышает остаток денежных средств каждого из клиентов. Также принимаем, что при остатке денежных средств m близкому к нулю изменение функции N(m,t) также стремится к нулю, т. е. клиенты не пытаются снять минимальные остатки денежных средств в копейках.
Теперь рассмотрим задачу в более общем виде. Предположим, что в рамках системы имеется P независимых проектов массового зачисления денежных средств. Каждый из проектов имеет свою клиентскую базу с резко отличающимися поведенческими свойствами. Тогда уравнения (1–2) необходимо рассматривать отдельно для каждого проекта p = 1…P. Кроме того, по аналогии с методикой [7] введем обратную связь, выраженную в управлении ресурсами кредитной организации на основе оперативной информации о суммарных остатках на счетах клиентов. Управление остатками выражается комплексом маркетинговых и экономических мер, направленных на изменение скорости снятия клиентами денежных средств за счет параметра . Запишем параметр как некоторую функцию B от изменения суммарного остатка денежных средств на счетах во времени. Учитывая уравнения (1–2), начальные и граничные условия, получаем следующую математическую модель.
|
|
(3) |
|
|
|
|
|
(4) |
|
|
|
|
|
(5) |
|
|
|
|
|
(6) |
|
|
|
|
|
(7) |
|
|
|
|
|
(8) |
Решение описанной математической модели может быть получено при помощи разностных методов [8]. Рассмотрим применение модели для конкретного банковского проекта по перечислению предприятием заработной платы на счета граждан.
Моделирование изменения остатков на счетах граждан. Предметом анализа выбран реальный проект. На банковские карточные счета работников некоторой организации зачисляется заработная плата. Важной бизнес-задачей для банка является оценка развития проекта, прогнозирование изменения остатков на счетах клиентов и сравнение полученных результатов с реальными данными. При этом обычное сравнение изменения остатков денежных средств с предыдущими периодами не дает полной картины, поскольку рассматриваемая организация состоит из социально различных групп работников, часть заработной платы которых может быть изменена либо переведена в другой банк.
Построенная модель (5–9) соответствует условиям описанной ситуации с коэффициентом p=1. При этом функция b(m, t,q) существенно зависит от различных групп клиентов. Проведем прогнозирование величины b(m, t,![]() ) на основе статистических данных по следующей методике.
) на основе статистических данных по следующей методике.
Расчетным периодом является 2006 г. Продемонстрируем методику расчета на основе одного месяца, например февраля 2006 г. Поскольку динамика совершения операций по пластиковым картам зависит от сезонности, и считаем, что на скорость снятия денежных средств клиентов существенно не влияют суммы зачисления, то функцию b(m, t,![]() ) целесообразно определить на основе данных предыдущего года, соответственно февраля 2005 г.
) целесообразно определить на основе данных предыдущего года, соответственно февраля 2005 г.
На рисунке 1 приведены графики изменения остатков на счетах сотрудников организации в течение февраля 2006 г. Все сотрудники разделены на группы сотрудников (далее – грейды), имеющих наиболее близкий размер заработной платы на момент зачисления 04.02.05. Количество грейдов эмпирически выбрано равным 7 с фиксированным интервалом в 5 условных единиц. Как видно из графика, наблюдается общая тенденция – наибольшую активность по снятию денежных средств клиенты проявляют в течение первых четырех дней. При этом поведение клиентов с разной заработной платой существенно разнится по суммам снимаемых денежных средств. Клиенты, получающие больше денежных средств, совершают операции на более крупные суммы денежных средств. С другой стороны, чем выше заработок клиентов, тем большая сумма остается в качестве остатков на их картсчетах. Кроме того, в зависимости от грейда существенно разнится характер снятия. Например, клиенты «старшего» грейда (более 30 условных единиц) в первые два дня незначительно снимали денежные средства, что связано с попаданием этих дней на выходные. Клиенты, имеющие небольшую заработную плату, начали активно снимать денежные средства в первые же часы после зачисления.

Рис. 1. Суммарные остатки денежных средств в условных единицах на картсчетах клиентов в разбивке по грейдам
Динамика снятия хорошо просматривается на графике изменения среднего снятия клиентами денежных средств за каждый из дней в течение рассматриваемого периода (рис. 2). Для наглядности график приведен для части грейдов и, по сути, представляет собой изменение суточной скорости снятия. Как видно из графика, скорость снятия существенно разнится как внутри грейда, так между грейдами. К примеру, суточная скорость снятия для «старшего» грейда (более 30 у. е.) в первые два дня не превышает 1 у. е./день, а уже 8.02.05 (после выходных дней) достигает 7 у. е./день.
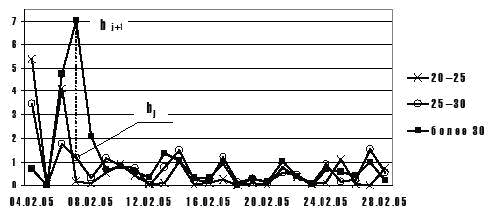
Рис. 2. Суточная скорость снятия денежных средств в условных единицах в разбивке по грейдам
Учитывая столь существенные изменения скорости снятия денежных средств в различных грейдах, для определения b(m, t,![]() ) для остатка денежных средств m в некоторый момент времени t первоначально определялись номера «ближайших» грейдов j и j+1 в феврале 2005 г., так чтобы выполнялось условие mj>m>mj+1 (остатки mj и mj+1 соответствуют средним остаткам грейда в соответствующий момент времени (рис. 1). Далее как среднее арифметическое вычислялась скорость снятия по следующей формуле.
) для остатка денежных средств m в некоторый момент времени t первоначально определялись номера «ближайших» грейдов j и j+1 в феврале 2005 г., так чтобы выполнялось условие mj>m>mj+1 (остатки mj и mj+1 соответствуют средним остаткам грейда в соответствующий момент времени (рис. 1). Далее как среднее арифметическое вычислялась скорость снятия по следующей формуле.
|
|
(9) |
Расчеты, проведенные на основе математической модели (3–8) с учетом уравнения скорости (9), позволили вычислить предполагаемое суммарное изменение остатков денежных средств на картсчетах сотрудников организации. Для проведения расчетов разработан комплекс программ, решение системы (3–9)осуществлялось при помощи разностных методов [8]. На рисунке 3 приведены расчетные и реальные графики изменения остатков на картсчетах в течение февраля 2006 г.

Рис. 3. Остатки денежных средств в условных единицах на счетах клиентов
Как видно из графиков, на первом этапе (первые 15 дней) наблюдается колебание реальных значений относительно расчетных в пределах 8% от суммы реальных остатков. Колебания вызваны недельными изменениями интенсивности снятия (особенно в выходные дни), поскольку вычисления скорости проводились на основе данных 2005 г. с отличием в днях недели. Между тем к концу расчета происходит уменьшение отклонений расчетных значений, что в целом подчеркивает соответствие динамики снятия денежных средств в феврале 2005 и 2006 гг.
На последнем этапе расчета (последние шесть дней) прогноз максимально соответствует реальным значениям, отклонение расчетных значений от реальных не превышает 3%. Таким образом, достигнута основная цель расчета, который показал соответствие между характером зачисления и динамикой снятия денежных средств в феврале 2005 и 2006 гг. Позднее полученный прогноз подтвердился информацией о развитии проекта в исследуемой организации.
Выводы:
|
1. |
Разработана математическая модель прогнозирования изменения остатков на счетах в рамках проектов массового зачисления денежных средств физическим лицам. |
|
2. |
Проведено прогнозирование изменения остатков на картсчетах сотрудников организации в рамках проекта по перечислению заработной платы в коммерческий банк. Проведенный расчет позволил достоверно оценить тенденции изменения работы организации в рамках проекта и определить предполагаемое суммарное значение остатка денежных средств на счетах сотрудников в конце расчетного периода. |
ЛИТЕРАТУРА
1. Иванов В.В. Оперативный анализ текущей ликвидности банка //Бухгалтерия и банки. 1999. № 4. С. 19–27.
2. Клесова Я.А. Управление активами и пассивами банков в условиях высоких трансакционных издержек. Финансы и кредит. 2006. №33. С. 8–16.
3. Вайдлих В. Социодинамика: системный подход к математическому моделированию в социальных науках. М.: Едиториал УРСС. 2004.
4. Маслов В.П. Квазистабильная экономика и ее связь с термодинамикой сверхтекучей жидкости. //Обозрение прикладной и промышленной математики. 2004. В. 4. Т. 11. С. 689–732.
5. Avrami M. Kinetics of Phase Change //J. Chemical Physics. 7. 12 (1939). Р. 1069.
6. Колмогоров А.Н. К статистической теории кристаллизации металлов //Изв. АН СССР. Сер. матем. 1937. №3, С. 355–358.
7. Дрозин А.Д. Теоретический анализ образования неметаллических включений в жидком металле //Изв. АН СССР. Металлы. 1987. № 6. С. 19–22.
8. Самарский А.А. Теория разностных схем. М.: Наука. 1989.