Опубликовано в журнале "Маркетинг в России и за рубежом" №2 год - 2003
ведущий специалист отдела внутреннего контроля
ООО «ЛУКОЙЛ-Севернефтепродукт»
Обычно в ходе аудиторских проверок всегда имеется возможность проанализировать, как влияет эластичность спроса покупателей на цены, издержки и финансовый результат организации. И что интересно: на предприятиях, относящихся к совершенно различным отраслям, в последние два года автору удавалось наблюдать одни и те же закономерности движения ценовых параметров под влиянием спроса. Думается, что они могут показаться интересными многим.
Пример 1. Имеется предприятие, относящееся к сфере материального производства. В табл.1 приводится динамика производства и реализации товара, выпускаемого предприятием, за 2000—2001 гг. (данные реальны).
Таблица 1
| Годы | Выручка от продаж (без НДС), тыс. руб. | Себестоимость, тыс. руб. | Объем продаж, шт. | Цена товара, тыс. руб. | Себестоимость единицы товара, тыс. руб. |
| 2000 | 358 945 | 147 844 | 67 341 | 5,33 | 2,20 |
| 2001 | 484 535 | 210 909 | 98 301 | 4,93 | 2,15 |
Примечания:
- цена товара (гр.4) может быть также найдена как отношение выручки от продаж (гр.1) к объему продаж (гр.3),;
- себестоимость единицы товара (гр.5) получена как отношение себестоимости (гр.2) к объему продаж (гр.2).
Как видно из табл. 1, в 2001 г. произошло снижение цены товара (с 5,33 до 4,93 тыс. руб. за единицу) при одновременном значительном росте объема продаж (с 67 341 до 98 301 единицы), то есть явно проявились признаки, что рынок становится эластичным (рис. 1).

Рис. 1. Зависимость объема продаж товара от цены
Если предполагать, что зависимость объема продаж у(х) от цены является линейной, то можно составить следующую функцию:
у(х) = kx + b,
где у(х) — объем продаж товара (шт.);
x — цена товара (тыс. руб. за единицу товара);
k и b — коэффициенты уравнения, значения которых требуется установить.
С помощью данных из табл. 1 составляется система линейных уравнений:
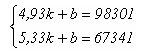
решение которой дает искомую зависимость (она изображена также на рис.1):
у(х) = –77400х + 47883. (1)
На самом деле зависимость (1) по мере роста цен или, наоборот, их снижения будет обладать свойством насыщения. При достижении определенного уровня цены как снизу, так и сверху данная зависимость станет нелинейной, когда объем продаж или очень мало зависит, или практически уже не зависит от изменения цены (впрочем, это вовсе не означает, что эффекта не будет — на линейном участке зависимости он сохранится, и вот на него-то и нужно делать ставку).
Кроме того, из табл. 1 следует, что в 2001 г. произошло также снижение себестоимости единицы товара (с 2,20 до 2,15 тыс. руб. за единицу) при одновременном росте объема продаж (с 67 341 до 98 301 единицы). Согласно теории финансового менеджмента это нужно понимать в том смысле, что зависимость себестоимости единицы товара от объема продаж формируется как функция переменных затрат (variable cost) и постоянных затрат (fixed cost), а потому данная зависимость будет выглядеть так:

где z(y) — себестоимость единицы товара (тыс. руб. на единицу товара);
FС — постоянные затраты (в тыс. руб.);
VС — переменные затраты (в тыс. руб.);
vc — удельные переменные затраты (тыс. руб. на единицу товара).
Опять же с помощью данных из табл. 1 составляется еще одна система уравнений:

откуда следует, что FС = 10 691 тыс. руб. и vc = 2,04 тыс. руб. на единицу товара.
Знание величин постоянных затрат и удельных переменных затрат, а также цены товара позволяет установить так называемую точку безубыточности. Для условий 2001 г. минимальный объем продаж ymin, при котором прибыль равна нулю, составит:
![]()
Таким образом, достигнутый в 2001 г. объем продаж (98 301 единица) более чем в 25 раз превышает безубыточный объем (3700 единиц). Разница очень большая, а это, согласно общим правилам финансового менеджмента означает, что фирма уже может позволить себе наращивать свою прибыль не только за счет повышения цен, а даже наоборот — за счет их снижения. Дело в том, что в условиях эластичного рынка снижение цен сопровождается ростом объема продаж, приводящим к росту выручки и прибыли.
Далее составляется функция зависимости себестоимости единицы товара z(y) от объема продаж у(х) (данная функция изображена на рис.2):
 (2)
(2)

Рис. 2. Зависимость себестоимости единицы товара от объема его продаж
Если в выражение (2) подставить вместо у(х) выражение (1), то получается уже зависимость себестоимости единицы товара z(y) от цены товара х:
![]() (3)
(3)
где z(y) — себестоимость единицы товара (тыс. руб. на единицу товара).
Построенный для зависимости (3) график (рис.3) наглядно показывает, как в условиях эластичного спроса снижение цены товара приводит к снижению себестоимости единицы товара.

Рис. 3. Зависимость себестоимости единицы товара от его цены
Далее, зная зависимость объема продаж у(х) от цены товара х, а также зависимость себестоимости единицы товара z(х) от цены х, выводится уже функция зависимости валовой прибыли P(х) от цены товара x:
![]() (4)
(4)
где P(x) — валовая прибыль от продажи товаров (в тыс. руб.).
Графическая интерпретация выражения (4), представленная на рис.4, имеет отчетливо выраженный максимум, означающий, что есть некоторая цена, обеспечивающая максимум прибыли для предприятия на рынке продаваемых им товаров.

Рис. 4. Зависимость валовой прибыли предприятия от цены товара
Для максимизации валовой прибыли P(x) осталось найти первую производную функционала (4), приравнять ее к нулю и решить полученное уравнение.
В итоге получаются следующие значения цены x, себестоимости z(x) и объема продаж y(x), обеспечивающие максимум валовой прибыли P(x) от реализации товара:
- цена единицы товара составит x = 4,12 тыс. руб., то есть 83,6% к уровню 2001 г.;
- объем продаж составит y(x) = 160 994 шт., то есть 63,8% к уровню 2001 г.;
- себестоимость единицы товара составит z(x) = 2,11 тыс. руб., то есть 98,1% к уровню 2001 г.;
- прибыль на единицу товара составит x – z(x) = 2,01 тыс. руб., то есть 72,3% к уровню 2001 г.;
- выручка от продаж составит хy(x) = 663,30 млн руб., или рост на 36,9% к уровню 2001 г.;
- валовая прибыль составит Р(x) = 323,60 млн руб., или рост на 18,3% против 2001 г.;
- наконец, рентабельность продаж составит 48,8% против 56,5% в 2001 г.
Если к этому добавить еще вывод о 25-кратном превышении достигнутого предприятием объема продаж по сравнению с точкой безубыточности, то ясно, что предприятие обладает очень большим потенциалом роста прибыли, для реализации которого нужно лишь незначительно — на 14% — снизить цены по сравнению с 2001 г.
Пример 2. Рассмотренный в примере 1 случай влияния эластичности спроса на цены, объем продаж и издержки является очень показательным, однако пока еще не самым распространенным случаем из жизни российских предприятий. Мало кто из них в настоящее время решается снижать цены, причем даже чуть-чуть. Обычно такое снижение цен является не столько стратегическим шагом, продиктованным целенаправленно осуществляемой маркетинговой политикой, сколько вынужденной реакцией предприятия на собственное же предыдущее слишком резкое повышение цен, которое отпугнуло покупателей (собственно говоря, именно это было причиной снижения цен в случае предприятия, показанного в примере 1).
В силу этого чаще всего пока приходится сталкиваться с ситуацией, которая приведена ниже в табл.2. На свой лад она тоже поддается исследованию методами теории финансового менеджмента, однако содержательная интерпретация решения является более замысловатой.
Таблица 2
| Годы | Выручка от продаж (без НДС), тыс. руб. | Себестоимость, тыс. руб. | Валовая прибыль, тыс. руб. | Объем продаж, тыс. кг | Цена товара, руб. | Себестоимость единицы товара, руб. | Удельная прибыль, руб. |
| 1999 | 10 095 | 7 643 | 2 452 | 754 | 13,39 | 10,14 | 3,25 |
| 2000 | 13 073 | 9 636 | 3 437 | 863 | 15,15 | 11,17 | 3,98 |
| 2001 | 16 043 | 12 357 | 3 686 | 899 | 17,85 | 13,75 | 4,10 |
Примечания:
- валовая прибыль (гр.3) представляет разницу между выручкой от продаж (гр.1) и себестоимостью (гр.2);
- цена товара (гр.5) может быть также найдена как отношение выручки от продаж (гр.1) к объему продаж (гр.4);
- себестоимость единицы товара (гр.6) получена как отношение себестоимости (гр.2) к объему продаж (гр.4);
- удельная прибыль (гр.7) вычисляется или как отношение валовой прибыли (гр.3) к объему продаж (гр.4), или же как разность цены товара (гр.5) и его себестоимости (гр.6).
В явном виде такого свойства эластичного рынка, как рост продаж при снижении цены (это имело место в примере 1), в табл.2 не наблюдается: объем продаж растет все три года (с 754 тыс.кг до 899 тыс.кг), несмотря на заметный рост цены (с 13,39 руб. до 17,85 руб.). Не видно и признаков, которые могли бы проявиться, если бы затраты на единицу выпускаемой продукции формировались как функция переменных затрат и постоянных затрат: в этом случае себестоимость единицы товара должна была бы снижаться, тогда как в табл. 2, наоборот, она растет (с 10,14 до
13,75 руб. за 1 кг).
Тем не менее ситуация для анализа вовсе не безвыходная. Заметный излом на рис. 5 подсказывает, что покупатель «устал» гнаться за ростом цены и для предприятия это обернулось меньшим приростом объема продаж, нежели в предыдущем году. Иными словами, эластичность спроса в действительности есть, только проявляется она в замедлении роста объема продаж.
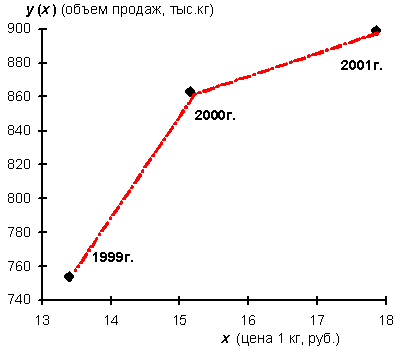
Рис. 5. Зависимость объема продаж товара от цены
В то же время рис.6 показывает, что меньший прирост объема продаж в 2001 г. по сравнению с предыдущим годом обусловил значительно больший прирост себестоимости 1 кг товара, а это есть опять же не что иное, как последействие все той же эластичности спроса, только проявившееся косвенно, в неявной форме. Если принять во внимание эти моменты, то появляется возможность выполнить анализ цен, объемов продаж и затрат, опираясь на функции, связывающие между собой уже не эти показатели непосредственно, а показатели их изменения во времени. С этой целью на основе табл.2 строится новая таблица — уже изменений объема продаж, цены и себестоимости единицы товара (табл. 3 и в качестве иллюстрации рис. 7—8).

Рис. 6. Зависимость себестоимости 1 кг товара от объема его продаж
Таблица 3
| Изменение объема продаж ∆y(∆x), тыс.кг. | Изменение цены за 1 кг ∆x, руб. | Изменение себестоимости 1 кг товара ∆z(∆x), руб. | |
| в 2000г. по сравнению с 1999г. | 109 | 1,76 | 1,03 |
| в 2001г. по сравнению с 2000г. | 36 | 2,70 | 2,58 |
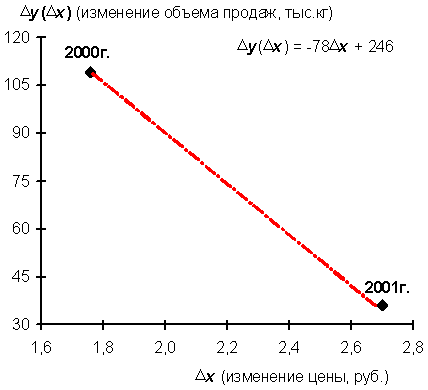
Рис. 7. Зависимость изменения объема продаж товара от изменения его цены
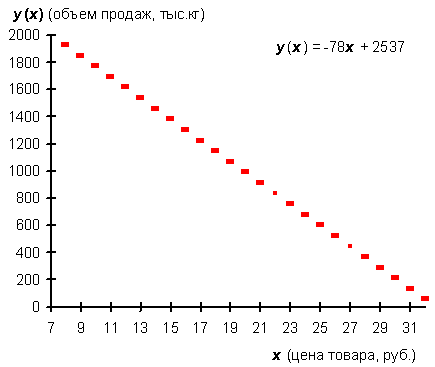
Рис. 8. Зависимость объема продаж товара от цены
Если исходить из наличия линейной зависимости между изменением объема продаж ∆y(∆x) и изменением цены ∆x, то можно написать уравнение
∆y(∆x) = k(∆x) + b,
где ∆y(∆x) — изменение объема продаж товара (тыс.кг);
(∆x) — изменение цены товара (руб.);
k и b — коэффициенты уравнения, значения которых требуется установить.
С помощью данных из табл. 3 составляется система линейных уравнений:
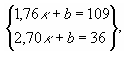
— решение которой дает нужную зависимость (она показана на рис. 7 в виде линии):
∆y(∆x) = –78∆x + 246. (5)
Применение преобразований x = x0 + ∆x, y = y0 + ∆y,
где x0 — базовая цена товара, подразумевающая цену последнего отчетного периода, то есть за 2001 г. Согласно табл.2 она составляет 17,85 руб. (табл. 2, гр. 5, нижняя строка);
y0 — базовый объем продаж здесь также за 2001 г., равный 899 тыс. кг (табл. 2, гр. 4, нижняя строка);
— позволяет осуществить переход от функции ∆y(∆x) к более удобной для анализа функции y(x), то есть к зависимости объема продаж непосредственно от цены товара x (эта зависимость изображена на рис. 8):
y(x) = –78x + 2537. (6)
Вместо линейной функции, представленной выражением (6), зависимость объема продаж от цены можно было бы значительно более точно аппроксимировать квадратным уравнением вида
![]()
где y(x) — объем продаж товара (тыс. кг);
x — цена товара (тыс. руб. за 1 кг);
a, b и c — коэффициенты уравнения, значения которых требуется установить.
В этом случае с помощью табл. 2 составляется система линейных уравнений с тремя неизвестными:

решение которой дает искомую функцию зависимости объема продаж y(x) от цены x:
y(x) = –12x2 + 411 –2595. (7)
Выражение (7) имеет максимум при цене 17 руб. за 1 кг и обеспечивает объем продаж 924 тыс.кг. Если сравнить эти показатели с достигнутыми в 2001 г., то выясняется, что оптимальный с точки зрения физического объема продаж уровень цены уже пройден: в 2001 г. цена была почти 18 руб. за 1 кг, при этом объем продаж составил 899 тыс.кг.
Но есть ли преимущество функции второй степени (7) перед линейной функцией (6)?
Если подходить к задаче исследования влияния эластичности спроса на объем продаж чисто математически, то да, пожалуй, есть. Однако если учесть маркетинговый и финансовый аспект интерпретации получаемых решений, то те общие выводы, которые следуют из простых линейных моделей, более важны, поскольку они позволяют не потерять видение и понимание ситуации в целом. Именно поэтому автор отдал предпочтение простым линейным конструкциям, пожертвовав малополезной в данном случае избыточной математической точностью квадратных или иных зависимостей.
Аналогичным образом — через линейную функцию — отыскивается зависимость изменения себестоимости ∆z(∆x) от изменения цены ∆x:
∆z(∆x) = k(∆x) + b,
где ∆z(∆x) — изменение себестоимости единицы товара (руб.);
∆x — изменение цены товара (руб.);
k и b — коэффициенты уравнения, значения которых требуется установить.
На основе данных табл. 3 составляется очередная система линейных уравнений:

решение которой имеет следующий вид (график изображен на рис. 9):
∆z(∆x) = 1,65∆x –1,87. (8)

Рис. 9. Зависимость изменения себестоимости 1 кг товара от изменения цены
Преобразования вида x = x0 + ∆x, z = z0 + ∆z,
где z0 — базовая себестоимость единицы товара (в рассматриваемой ситуации за 2001 г.), равная 13,75 руб. (табл. 2, гр. 6, нижняя строка);
— позволяют перейти от функции ∆z(∆x) к более удобной для анализа теоретической функции z(x), то есть к зависимости себестоимости непосредственно от цены товара x (данная зависимость представлена на рис. 10):
∆z(∆x) = 1,65x + 17,57. (9)

Рис. 10. Зависимость себестоимости 1 кг товара от цены
Если цена товара x будет меньше 10,65 руб., то из выражения (9) следует ... отрицательное значение себестоимости (это очень хорошо видно на рис.10). Дело в том, что в примере 2 в составе затрат не была выделена такая составляющая, как постоянные затраты FC, и соответственно это привело к столь странному результату. Если же было бы возможно учесть в составе себестоимости товара наличие постоянных затрат, то график на рис.10 выглядел бы аналогично рис.3, то есть по мере уменьшения цены x асимптотически приближался бы к величине удельных переменных затрат vc; сейчас же этого не происходит. А потому, говоря об использовании функций ∆z(∆x) и z(x) для каких-либо расчетов, нужно иметь в виду, что это справедливо лишь по отношению к тому интервалу изменения цены ∆x, который имел место в 1999—2001 гг. (табл. 3), то есть от 1,7 руб. до 2,8 руб.
Поскольку в примере (2) затраты не удается разложить на постоянные и переменные, то в силу этого невозможно представить зависимость себестоимости единицы товара от объема продаж как гиперболическую. Если в выражение (9) преобразовать с помощью функционала (6), подставив вместо x выражение для y(x), то получается только линейная зависимость, но, правда, знаком минус перед объемом продаж она показывает, что при росте объема продаж себестоимость единицы товара будет обязательно снижаться:
z(y) = –0,021y(x) + 36,01. (10)
На очереди определение зависимости валовой прибыли P(∆x) от изменения цены ∆x товара и выявление, при каком значении аргумента данная функция имеет максимум.
Эта зависимость, получаемая на основе выражений (5) и (8), будет выглядеть следующим образом (график представлен на рис. 11):
![]() (11)
(11)
где P(∆x) — валовая прибыль от продажи товаров (в тыс. руб.).
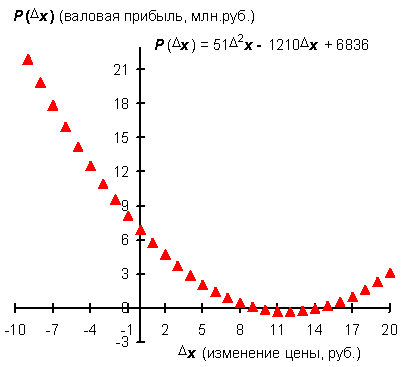
Рис. 11. Зависимость объема валовой прибыли от изменения цены
Преобразование x = x0 + ∆x позволяет перейти от функции P(∆x) к функции P(x), то есть уже к зависимости валовой прибыли непосредственно от цены товара x (рис. 12):
P(∆x) = 51x2 – 3046x + 45140. (12)

Рис. 12. Зависимость объема валовой прибыли от цены товара
Для максимизации валовой прибыли P(∆x) или же P(x), как и в примере 1, следовало бы найти точки экстремума данных функций. Но хитрость здесь в том, что выражения (11) и (12) представляют собой уравнения парабол с положительным значением постоянного коэффициента при переменной во второй степени (+51), то есть парабол, экстремумами которых являются точки минимума (рис. 11—12). А это означает, что ответ на вопрос, при каком изменении цены ∆x или же при какой цене x валовая прибыль P(x) будет максимальна, получить не удастся. Вместо этого можно лишь узнать, при каком изменении цены ∆x или соответственно при какой цене x будет получен максимальный убыток, но это интересует предпринимателя меньше всего. Как же быть?
Может возникнуть ироничный вопрос: а как же быть с огромной положительной валовой прибылью, которая согласно графику на рис.12 и функции тренда на графике имеет место быть даже при нулевой цене на товар? Эта странная ситуация возникает вследствие того, что была использована, как уже говорилось выше, линейная, а не гиперболическая, аппроксимация тренда затрат (то есть не бралось во внимание наличие постоянных затрат FC). В результате это становится причиной возникновения отрицательных значений себестоимости, а также положительной прибыли при нулевой цене. Следовательно, говоря об использовании функций P(∆x) и P(x) для каких-либо прогнозов, равно как и функций ∆z(∆x) и z(x), опять же нужно иметь в виду, что эти прогнозы будут справедливы лишь по отношению к тем интервалам изменения цены ∆x, которые имели место в 1999—2001 гг. (табл. 2—3). При выходе изменения цены ∆x за рамки этих интервалов, на которых были получены функционалы (11) и (12), изображенные также на рис. 11—12 (при выходе как вниз, так и вверх), полученные зависимости становятся непригодными для анализа и прогнозирования.
Итак, какой же следует вывод из примера 2? В отличие от примера 1, где сразу же был получен ценовой ориентир, обеспечивающий максимум валовой прибыли, здесь приходится довольствоваться знанием того, что чем меньше вырастет цена (а лучше, если она даже несколько снизится), тем:
- больше будет объем продаж (об этом говорят выражения (5—6) и рис. 7—8);
- меньше окажется себестоимость единицы товара (уравнения (9—10) и рис. 9—10);
- и соответственно выше будет прибыль предприятия (формулы (11—12) и рис. 11—12).
Но достаточны ли такие, на первый взгляд, расплывчатые рекомендации, если рассматривать их с точки зрения применения в маркетинговой политике предприятия?
Разумеется. Ведь если руководству предприятия хватит смелости действительно попробовать увеличить прибыль предприятия не числом (за счет повышения цен), а умением (за счет пусть незначительного, но все же снижения этих цен), то результаты не заставят себя долго ждать. Благодарный рынок тут же продемонстрирует такое свое качество, как эластичность спроса. Даже на символическое снижение цены потребитель ответит незамедлительным ростом спроса, обеспечивающим для предприятия рост объема продаж. А это обусловит уже остальные позитивные для предприятия финансовые последствия, в том числе снижение себестоимости единицы товара и рост прибыли, то есть повышение экономичности производства в целом. Более того, сразу же обнаружится, как ситуация, показанная в примере 2, плавно перерастет в ситуацию, близкую к приведенной в примере 1, и станет доступной для определения такой цены, которая обеспечит предприятию максимум прибыли.
Вывод
Приведенные два примера, несмотря на свою, казалось бы, скромность (два предприятия — это действительно не так уж и много), тем не менее актуальны.
Во-первых, это не совсем рядовые предприятия, а юридические лица, находящиеся под бдительным наблюдением Антимонопольного комитета. Во-вторых, товары, производство и продажа которых рассматривались в примерах, это товары, являющиеся важными для любой страны, а для нашей страны особенно, в силу специфики ее экономического развития, географии и истории. В-третьих, ситуацию, описанную в примере 2, автору удалось уже заметить на десятке предприятий, принадлежащих совершенно различным отраслям сферы материального производства, из чего следует вывод, что эластичность спроса на потребительском рынке становится массовым явлением.
Как можно было бы воспользоваться этим свойством рынка?
Пусть несколько десятков крупных и средних предприятий в различных отраслях подадут пример снижения цен, преследуя при этом, казалось бы, более чем меркантильную цель — увеличить объемы продаж и свою прибыль. В таком снижении цен не было бы ничего удивительного: на дефляцию правительство рассчитывает уже не первый год, только до сих пор этого не произошло.
Эффект снижения цен даже отдельными предприятиями будет аналогичен тому, который наблюдают, бросая камень в воду: камень падает в одну точку, а волны разбегаются по всей глади пруда. Так и с ценами: снижать их начинают лидеры, а последователями становятся все.
Литература
- Корн Г., Корн Т. Справочник по математике. — М.: Наука, 1984. — 832 с.
- Ланге О., Банасиньский А. Теория статистики. — М.: Статистика, 1971. — 400 с.
- Поллард Дж. Справочник по вычислительным методам статистики. — М.: Финансы и статистика, 1982. — 344 с.
- Стоянова Е.С. Финансовый менеджмент: теория и практика. — М.: Перспектива, 2000. — 574 с.
- Четыркин Е.М. Статистические методы прогнозирования. — М.: Статистика, 1977. — 200 с.
- Четыркин Е.М., Калихман И.Л. Вероятность и статистика. — М.: Финансы и статистика, 1982. — 319 с.
- Четыркин Е.М. Методы финансовых и коммерческих расчетов. — М.: Дело ЛТД, 1995. — 320 с.

